آزمون میانگین نمونه‌ تکی در SPSS

تعریف آزمون میانگین نمونه‌ تکی در SPSS:

 با یک نمونه از جامعه آماری سروکار خواهیم داشت. قرار است براساس این نمونه در مورد میانگین جامعه قضاوت انجام گیرد.

فرض کنید به عنوان یک تحلیل‌گر داده (Data Scientist)، با یک جامعه‌ آماری مواجه شده‌اید که میانگین آن مشخص نیست و می‌خواهید در مورد این میانگین، تحقیق و بررسی انجام دهید و به یک تصمیم برسید.

 مثال:

در نظر بگیرید که در یک کارخانه تولیدی لبنیات، شکایاتی مبنی بر کم بودن وزن بسته‌های پنیر دریافت شده است. مسئولین برای آنکه مشخص کنند آیا شکایات معتبر یا بی‌دلیل هستند دست به نمونه‌گیری زده‌اند و براساس اطلاعاتی که از وزن بسته‌های پنیر در نمونه وجود دارد، می‌خواهند به این تصمیم آماری برسند که آیا دستگاه‌ها احتیاج به تنظیم دارند یا شکایات بی‌مورد هستند.

پیش فرض‌های تحلیل t تک نمونه ای یا تی تک گروهی

۱- توزیع داده‌ها باید نرمال باشد (با استفاده از آزمون کولموگروف اسمیرنوف).

۲- داده‌ها باید در مقیاس فاصله‌ای یا نسبی باشند (ماننده نمره سن، وزن، پرسشنامه و …).

۳- نمره معیار یا ثابتی باشد که بتوانید میانگین خود را با آن مقایسه کنید.

اجرای تحلیل t تک نمونه ای یا تی تک گروهی

فرض کنید نمره افسردگی چند نفر را با پرسشنامه افسردگی بک به دست آورده‌اید. طبق دستورالعمل این پرسشنامه افرادی که نمره ۲۰ و بالاتر را کسب کنند دارای افسردگی هستند. حالا شما می‌خواهید نمره‌ای که به دست آوردید را با این عدد ثابت ۲۰ مقایسه کنید. برای این کار در منوی بالای SPSS به مسیر زیر بروید:

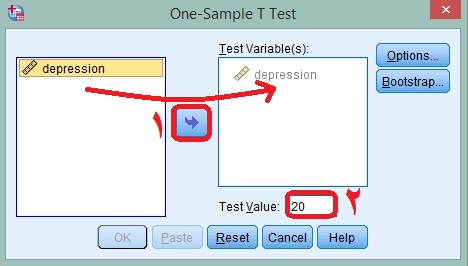
Analyze>Compare Means>One-Sample T Test

پس از رفتن به مسیر ذکر شده کادر زیر برای شما باز خواهد شد. در کادر زیر نمره افسردگی را از کادر سمت چپ به کادر سمت راست انتقال می‌دهیم.  سپس در کادر Test Value که در شکل زیر با عدد ۲ مشخص شده است نمره ثابت یا معیار را که در اینجا ۲۰ است وارد می‌کنیم و بر روی گزینه Ok کلیک می‌کنیم.

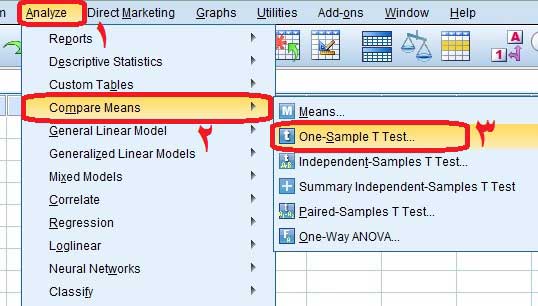
پس از مرحله بالا خروجی داده‌ها ظاهر می‌شود. در بین جداول، نمرات و اعداد مشخص شده به رنگ قرمز موررد نظر ما هستند و در جدول خروجی گزارش می‌شوند. همانگونه که در جدول زیر مشاهده می‌شود میانگین به دست آمده از جانب ما از نمره ثابت به طور معناداری بیشتر است.

(نحوه گزارش خروجی تحلیل t تک نمونه ای یا تی تک گروهی در SPSS)

1. پیش‌نیازهای ضروری برای آزمون میانگین نمونه تکی (One Sample T Test)

قبل از هر چیز باید از شرایط و فرضیاتی که آزمون میانگین نمونه تکی باید داشته باشد مطلع باشیم. در زیر فهرستی از این فرضیات دیده می‌شود:

• داده‌ها کمی (عددی) هستند.
• توزیع جامعه آماری نرمال است.
• واریانس جامعه آماری ثابت ولی نامعلوم است. این پارامتر باید توسط مشاهدات نمونه‌ای محاسبه یا برآورد شود.

نکته:

اگر حجم نمونه کم (حدود ۳۰) و میزان چولگی، کم باشد، باز هم می‌توان از آزمون میانگین نمونه‌ تکی برای قضاوت در مورد میانگین جامعه استفاده کرد.

فرض‌ها و آماره آزمون

در انجام آزمون میانگین نمونه‌ تکی، فرض‌های صفر و مقابل به صورت زیر در نظر گرفته می‌شوند:

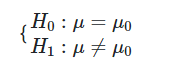
مقدار $${\mu }_{\mathrm{۰}}$$ همان مقداری است که به نظر می‌رسد باید میانگین جامعه آماری داشته باشد. حتی می‌توان آن را به عنوان حدس اولیه برای میانگین جامعه در نظر گرفت. مشخص است که در فرض مقابل یا $$H_1$$ این تصور به چالش کشیده شده است. آماره آزمون، در ادامه معرفی شده و دارای توزیع t student است.

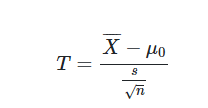
نکته: در نرم‌افزار SPSS فرضیات، به صورت زیر در نظر گرفته می‌شوند. ولی به هر حال نتیجه حاصل، در هر دو حالت یکسان خواهد بود.

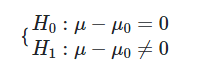
با توجه به خصوصیاتی که مقدار احتمال (p-value) دارد، اگر نتیجه آن برای آزمون کمتر از احتمال خطای نوع اول () یا همان سطح خطای آزمون شود، فرض صفر را رد خواهیم کرد.

شیوه اجرای آزمون میانگین نمونه تکی در SPSS

برای اجرای این آزمون طبق معمول از فهرست Analysis شروع می‌کنیم سپس گزینه Compare Means و دستور One Sample T-test را انتخاب کرده و پارامترهای آزمون را مطابق تصویرهای زیر تنظیم خواهیم کرد.

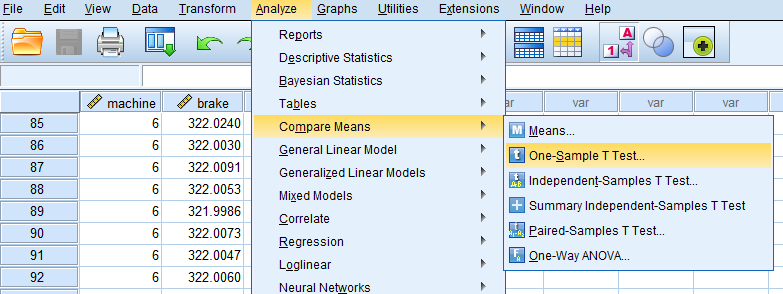
در تصویر زیر هر یک از پارامترهای مربوط به این آزمون، معرفی شده‌اند. توجه داشته باشید که متغیرهایی که در قسمت (Test Variable(s قرار می‌دهید، مقدارهای عددی یا متغیر کمی باشند.

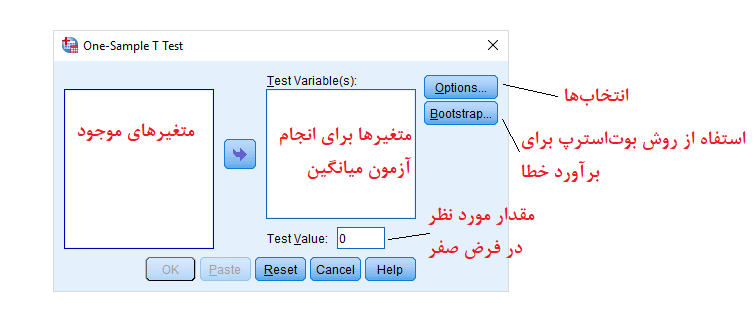
در خروجی این آزمون، یک فاصله اطمینان برای اختلاف میانگین جامعه از $${\mu }_{\mathrm{۰}}$$ نیز ایجاد می‌شود. سطح اطمینان برای این فاصله اطمینان را با انتخاب دکمه Options می‌توان تعیین کرد.

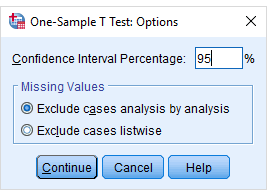
همینطور اگر چندین متغیر را در بخش متغیرهای آزمون قرار داده‌اید، با انتخاب گزینه‌ Exclude cases analysis by analysis مشخص می‌کنید که داده‌های گمشده (Missing Values) در هر تحلیل جداگانه در نظر گرفته شود.

برای مثال اگر برای متغیر اول،‌ مشاهده سوم و برای متغیر دوم، مشاهده پنجم دارای مقدار گمشده است، هنگام اجرای آزمون برای متغیر اول، مشاهده سوم و برای آزمون میانگین متغیر دوم،‌ مشاهده پنجم در نظر گرفته نخواهد شد. ولی با انتخاب Exclude cases listwise فقط مشاهداتی در انجام همه آزمون‌ها به کار می‌روند که مقدار گمشده در هیچ یک از آن‌ها وجود ندارد. بنابراین با انتخاب این گزینه، مشاهده سوم و پنجم در تحلیل به کار نخواهند رفت.

مثال ۲

فرض کنید اطلاعات مربوط به وزن ۲۰ بسته ۷۵۰ گرمی پنیر تولیدی در یک کارخانه در اختیار شما قرار گرفته است. باید قضاوت کنید که آیا این نمونه در مورد شکایت مشتریان مبنی بر کم بودن وزن بسته‌ها دلیل خوبی است یا شکایت‌ها بی‌مورد هستند؟ این اطلاعات را در SPSS مطابق تصویر زیر وارد کرده‌ایم.

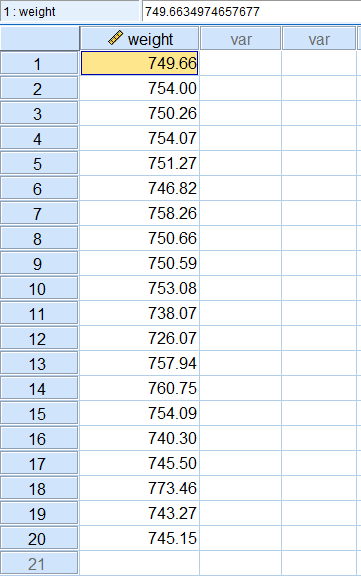
برای آنکه مشخص شود توزیع این داده‌ها شبیه نرمال هستند، از یک «بافت‌نگار فراوانی» (Histogram) استفاده می‌کنیم. برای ترسیم آن از فهرست Analysis گزینه frequency را انتخاب و در پنجره ظاهر شده تنظیمات را مطابق با تصویرهای زیر پیاده می‌کنیم.

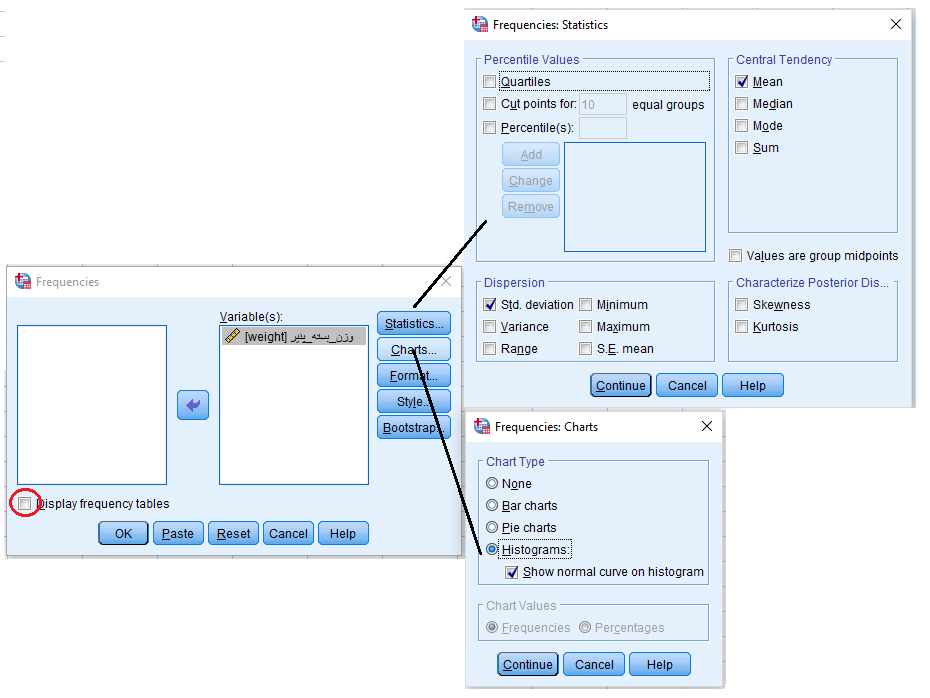
نکته:

از آنجایی که احتیاجی به مشاهده جدول فراوانی وجود ندارد، گزینه display frequency tables را از حالت انتخاب خارج کرده‌ایم.

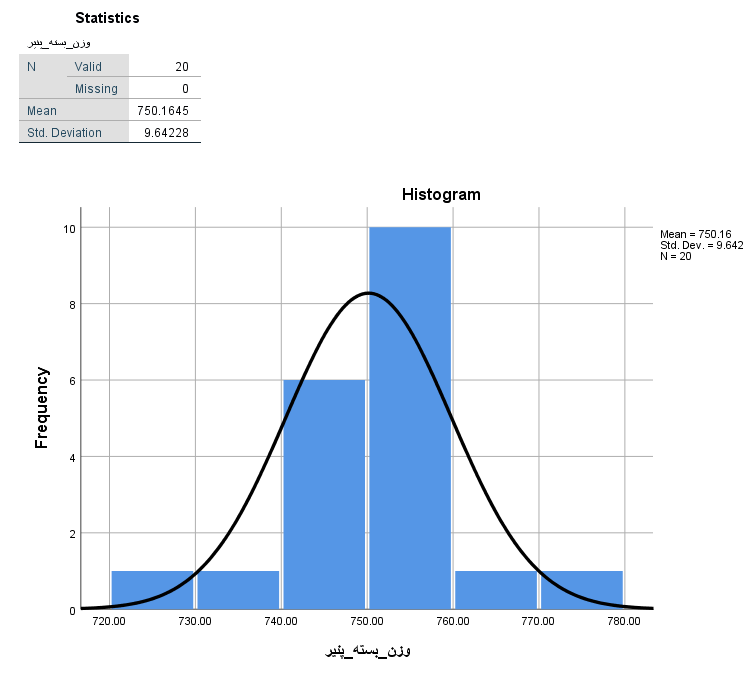
(خروجی به صورت زیر در خواهد آمد.)

• حال مراحل دسترسی به آزمون میانگین نمونه تکی را طی کرده و پارامترها را مطابق تصویر زیر در پنجره مربوط به آزمون تنظیم می‌کنیم.

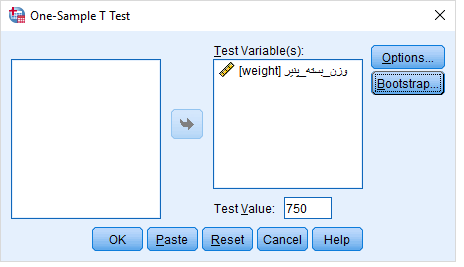
• با فشردن دکمه OK محاسبات صورت گرفته و خروجی مطابق با جدول زیر ظاهر خواهد شد.

1. در جدول اول با عنوان One-Sample Statistics،

2. میانگین نمونه برابر با ۷۵۰٫۱۶۴۵ گرم

3. با انحراف استاندارد  ۹٫۶۴۲۲۸ گرم

4. خطای استاندارد میانگین نیز برابر با ۲٫۱۵۶۰۸ گرم

• در جدول دوم، آزمون آماری با فرض صفر:

1.  مقدار آمار آزمون ۰٫۰۷۶ و درجه آزادی نیز ۱۹ بدست می آید.

2. با توجه به بزرگ بودن مقدار احتمال (p-Value) که در SPSS با Sig نمایش داده می‌شود و مقایسه آن با احتمال خطای نوع اول دلخواه $$\alpha$$ (که معمولا آن را ۰٫۰۵ در نظر می‌گیریم)

3. متوجه می‌شویم که ادعا مشتریان نادرست است چرا؟

4. زیرا ۰٫۹۴۰ بزرگتر از ۰٫۰۵ است. در نتیجه این نمونه دلیلی بر رد فرض صفر ارائه نکرده است و نمی‌توان فرض صفر را رد کرد.

مثال ۳:

.فرض کنید دو نوع محصول A و B در بسته‌های ۷۵۰ گرمی تولید شوند.

از هر دو محصولات آزمون می گیریم که متوسط وزن بسته‌ها همان ۷۵۰ گرم است.

ولی بنا به دلایلی (مثلا باز بودن بسته بندی و خارج شدن محتویات از بسته‌ها) در هر دو نمونه یک مقدار گمشده وجود دارد.

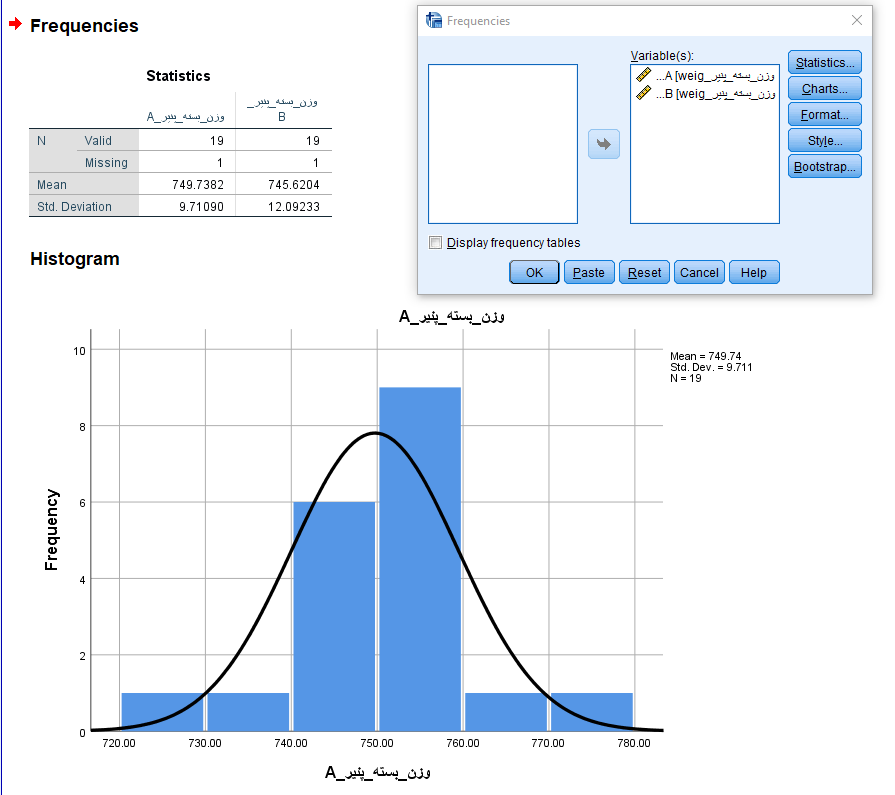
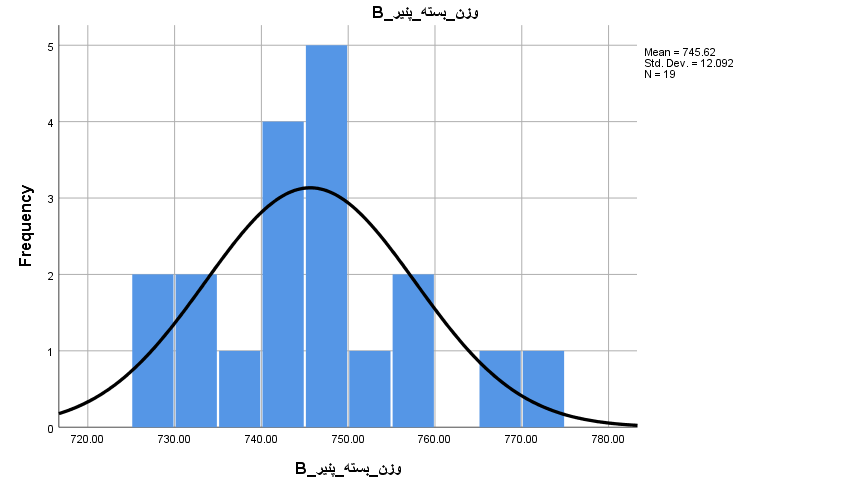
حال آزمون را با دو وضعیت برای داده‌های گمشده اجرا می‌کنیم. در حالت اول گزینه Exclude cases analysis by analysis را در بخش option فعال کرده و نتایج آزمون را مشاهده می‌کنیم.

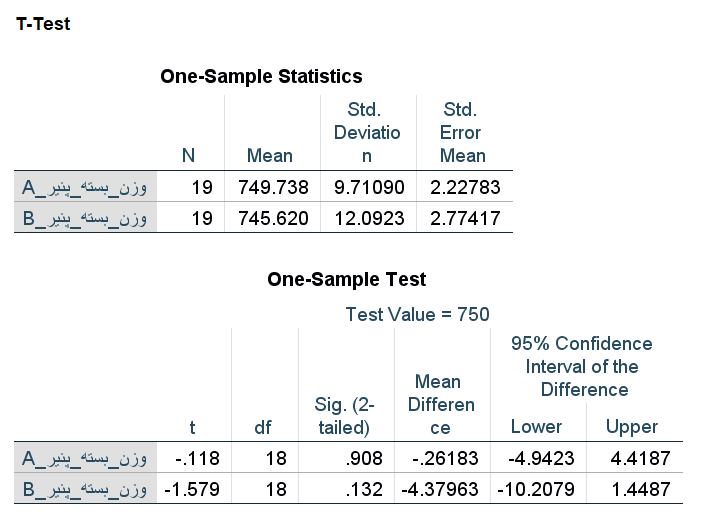
از آنجایی که هر کدام از متغیرها یا ستون‌ها دارای یک مشاهده گمشده بودند، تعداد در جدول اول برابر با ۱۹ ثبت شده است.

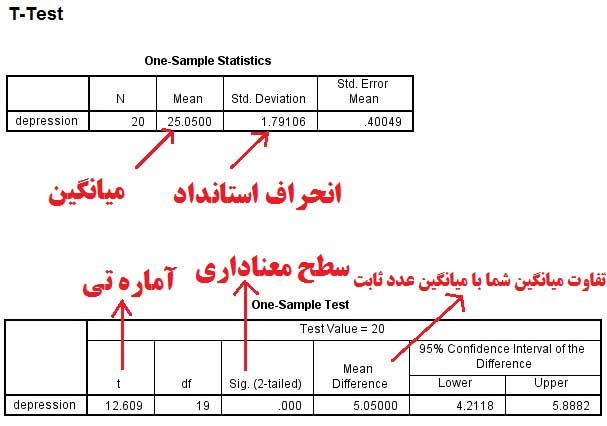
همچنین در جدول دومی SIG،  فرض صفر در سطح خطای ۰٫۰۵، توسط این نمونه‌ها رد نخواهد شد و به نظر می‌رسد میانگین وزن بسته‌ها همان ۷۵۰ گرم ادعای کارخانه است.

نکته :اگر لازم باشد که هر دوی مشاهدات گمشده در متغیرها کارخانه لحاظ نشوند چه کار باید انجام داد؟

کافی است که گزینه Exclude cases listwise را از بخش options انتخاب و آزمون را اجرا کنید.

خروجی در این حالت به صورت زیر در خواهد آمد. مشخص است که در جدول اول، تعداد مربوط به هر دو گروه ۱۸ خواهد بود و درجه آزادی (df) مربوط به آماره آزمون هم ۱۷ محاسبه می‌شود.

نکتهمهم:تغییر مقدار میانگین در هر دو متغییر فوق:

۱-  تعداد مشاهدات متفاوت است، میانگین نیز  بر اساس آن تغییر کرده است.

۲-چرا در کار خانه وزن بسته‌های محصول B کمتر از ۷۵۰ گرم است؟

زیرا مقدار Sig در سطر دوم با احتساب داده‌های گمشده برای هر دو گروه کمتر از ۰٫۰۵ است. بنابراین فرض صفر رد می شود یعنی میانگین بسته‌های محصول B مخالف ۷۵۰ گرم است.

از طرف دیگر چون فاصله اطمینان شامل ناحیه منفی است مشخص می شود که تفاضل میانگین وزن بسته‌ها از ۷۵۰ گرم دد ۹۵٪ مواقع کمتر از صفر است. به این ترتیب مشخص است که وزن بسته‌ها کمتر از ۷۵۰ گرم است و دستگاه‌های مربوط به بسته‌بندی باید تعمیر و تنظیم شوند.

09357258425 

www.pajuha.ir

[e-mail]

سفارش ترجمه تخصصی