آموزش اجرای آزمون فریدمن در SPSS

 تعریف :

آزمون فریدمن (Friedman) برای طرح­ های درون گروهی (نمونه ­های وابسته) مناسب است. آزمون فریدمن تعمیم ­یافته آزمون ویلکاکسون است و معادل ناپارامتریک آزمون اندازه ­های مکرّر­ است. در این آزمون ما یک گروه از افراد یا آزمودنی داریم که در حداقل دو وضعیت یا دو مقطع زمانی مختلف مورد­سنجش قرار گرفته ­اند.

هدف آزمون فریدمن در spss:

• هدف این است که تغییرات نمرات (میانه) را در چند (۲ و بیشتر) وضعیت یا مقطع زمانی مقایسه کنیم.
• سطح سنجش متغیر در این آزمون باید ترتیبی باشد.
• پژوهش­گران عموما از این آزمون جهت رتبه ­بندی یا اولویت­ بندی متغیرها استفاده می ­کنند.

کاربرد آزمون فریدمن:

این آزمون زمانی بکار می رود که مقیاس اندازه گیری حداقل در سطح مقیاس ترتیبی باشد. این آزمون مشابه کروسکال والیس است، با این شرط که K گروه نمونه جور شده باشند.

نکته:

توان آزمون فریدمن در مقایسه با قویترین آزمون پارامتری برای K گروه مستقل یعنی آزمون F یکسان است. آزمون فریدمن برای تجزیهء واریانس دوطرفه (برای داده های ناپارامتری) از طریق رتبه بندی به کار می رود.

مثال:
پژوهشی با هدف تعیین و رتبه ­بندی“مهم ­ترین ویژگی ­های اساتید دانشگاه“در دانشگاه شیراز انجام شد و در آن از ۱۰۰ دانشجوی دکتری دانشگاه شیراز پرسیده شد که نظر خودشان را در ارتباط با هرکدام از ویژگی­ های مطرح شده اساتید در پرسشنامه ابراز کنند. از دانشجویان پرسیده شد که تا چه­ حد به هرکدام از ویژگی­ های اساتید اهمیت می­ دهند؟ پنج ویژگی­ مطرح شده در ارتباط با اساتید عبارتند از: تسلط علمی، اخلاق خوب در روابط با دانشجویان، ظاهر مرتب و آراسته، فن بیان مناسب و رعایت انصاف در نمره­ دهی. دانشجویان به هرکدام از ویژگی­ های مطرح شده در قالب طیف ۱۱ گزینه­ ای (از ۰ تا ۱۰ که نمره بالاتر به معنای اهمیت بیشتر است) نمره دادند.

بر این اساس سوال زیر طرح و آزمون شد:
کدام ویژگی­ های اساتید اهمیت بالاتری برای دانشجویان دارد؟
با استفاده از آزمون فریدمن سوال مطرح شده را ارزیابی می­کنیم.

نحوه اجرا:
مسیر زیر را دنبال می­کنیم:

Analyze —>Nonparametric Tests —>Legacy Dialogs —>K Related Samples

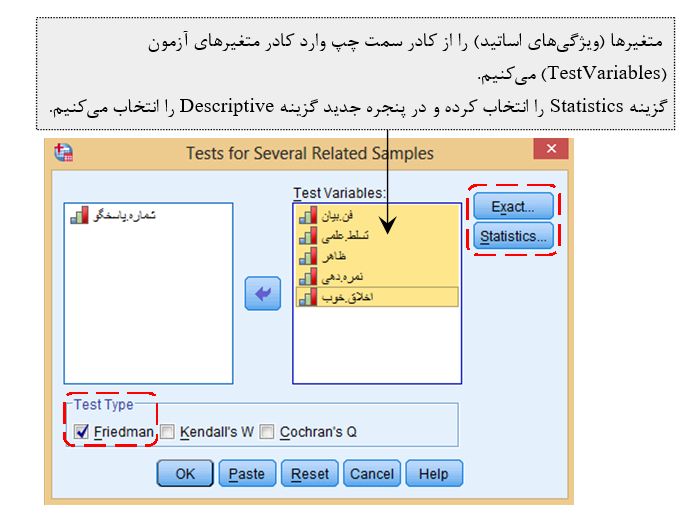
نتیجه بدست آمده:
در جدول بعد میانگین و انحراف استاندارد متغیرها ارائه شده است. دامنه میانگین از ۰ تا ۱۰ است.

مقایسه میانگین ویژگی­ های اساتید نشان می­ دهد که بالاترین میانگین (۷٫۷۹) متعلق به ویژگی انصاف در نمره ­دهی و پایین ­ترین میانگین (۳٫۳۱) متعلق به ویژگی ظاهر آراسته است. جهت بررسی معنی­ دار بودن تفاوت بین ویژگی­های اساتید و رتبه ­بندی مهم­ ترین ویژگی­ های اساتید از نظر دانشجویان، باید نتایج جدول آخر (Test Statistics) را بررسی کنیم.

Descriptive Statistics
	N	Mean	Std. Deviation	Minimum	Maximum
فن بیان	۱۰۰	۴٫۹۹	۱٫۸۳	۲	۹
تسلط علمی	۱۰۰	۴٫۴۸	۱٫۶۶	۲	۱۰
اخلاق خوب	۱۰۰	۵٫۰۱	۱٫۷۹	۲	۱۰
انصاف در نمره دهی	۱۰۰	۷٫۷۹	۱٫۵۵	۵	۱۰
ظاهر آراسته	۱۰۰	۳٫۳۱	۲٫۰۱	۰	۸

جدول زیر وضعیت رتبه ­بندی متغیرها (ویژگی­های اساتید) را نشان می­ دهد.

میانگین رتبه (Mean Rank):

مقایسه میانگین رتبه ها نشان می ­دهد که بالاترین میانگین رتبه (۴٫۵۸) به ویژگی انصاف در نمره ­دهی اختصاص دارد و که بدین معناست که مهم ­ترین ویژگی استاد از نظر دانشجویان ویژگی انصاف در نمره­ دهی است.

بعد از ویژگی فوق، مهم ­ترین ویژگی اساتید به ترتیب شامل ویژگی­ های فن بیان مناسب، اخلاق خوب در روابط با دانشجویان، تسلط علمی و ظاهر مرتب و آراسته می­ شود.

لازم به ذکر است که میانگین رتبه با میانگین حسابی تفاوت دارد و نحوه محاسبه این دو میانگین متفاوت است.

Ranks
	Mean Rank
فن بیان	۳
تسلط علمی	۲٫۵۶
اخلاق خوب	۲٫۹۳
انصاف در نمره ­دهی	۴٫۵۸
ظاهر آراسته	۱٫۹۴

 مهم ­ترین جدول آزمون فریدمن :

• که قبل از تفسیر جداول دیگر نخست باید نتایج این جدول را ارزیابی کرد و در صورت معنی­ دار بودن آزمون فریدمن، به تفسیر نتایج جداول توصیفی و میانگین رتبه بپردازیم.
• این جدول معنی ­داری آماری را نشان می ­دهد. مقدار مجذور کای به دست آمده برابر با ۱۶۳٫۷ است که در سطح خطای کمتر از ۰۵/. قرار دارد (۰۵/.­>P).
• معنی­ دار بودن آزمون فریدمن بدین معناست که رتبه­ بندی ویژگی­های اساتید از نظر دانشجویان بامعناست و دانشجویان رتبه ­بندی متفاوتی از ویژگی­ های اساتید دارند.

Test Statisticsa
N	۱۰۰
Chi-Square	۱۶۳٫۷۵
df	۴
Asymp. Sig.	۰۰۰٫
a. Friedman Test

گزارش:
از آزمون فریدمن برای رتبه ­بندی مهم ­ترین ویژگی ­های اساتید استفاده شد. آزمون فریدمن نشان داد که اهمیت و رتبه ویژگی­ های مطرح ­شده در مورد اساتید با یکدیگر متفاوت است(۰۰۱/. >P، ۴ = df، ۱۶۳٫۷۴= مجذور کای).
مقایسه میانگین رتبه­ ها نشان می­دهد که مهم ­ترین ویژگی اساتید از نظر دانشجویان به ترتیب ویژگی انصاف در نمره ­دهی، فن بیان مناسب و اخلاق خوب در روابط با دانشجویان است. میانگین رتبه این ویژگی­ ها به ترتیب ۴٫۵۸، ۳ و ۲٫۹۳ است(میانگین رتبه همه ویژگی­ها را در یک جدول گزارش کنید).

09357258425 

www.pajuha.ir

[e-mail]

سفارش ترجمه تخصصی

همه چیز درباره آزمون T مستقل در spss

آزمون T مستقل

آزمون T مستقل به ارزیابی مسئله ها  می پردازد که آیا میانگین یا معدل دو گروه یا دو وضعیت از لحاظ آماری تفاوتی با هم دارند یا نه.

این آزمون‌، از آزمون‌های قدرتمند محسوب می‌شوند که برای داده‌های پارامتری و داده‌هایی که معمولاً توزیع می‌شوند استفاده می‌گردند.
نکته:

از آزمون‌های t برای تحلیل آزمایشات ساده یا انجام مقایسات ساده بین سطوح متغیر وابسته استفاده می‌شود.

آزمون t بر دو قسم است:

۱) آزمون t وابسته                                     ۲) آزمون t اندازه‌گیری مکرر( که به آن آزمون t نمونه‌های جفت یا مرتبط نیز گفته می‌شود)

تعریف آزمون t  وابسته:

در صورتی که شما دو گروه جدا از افراد یا موردهایی را در یک طرح بین شرکت‌کنندگان (مثل زن و مرد، گروه آزمایش و کنترل) داشته باشید استفاده می‌شود.

تعریف آزمون t اندازه‌گیری مکرر( که به آن آزمون t نمونه‌های جفت یا مرتبط نیز گفته می‌شود):

در شرایطی استفاده می‌شود که شرکت کنندگان داده‌هایی برای تمام سطوح و وضعیت متغیر مستقل در یک طرح درون-شرکت کنندگان ارائه می‌دهند (مثلاً قبل یا بعد از مداخله).

در این نوشته آموزش آزمون t مستقل را فرا خواهیم گرفت. در مطلب دیگری به آزمون t اندازه‌گیری‌های مکرر پرداخته خواهد شد. دلیل اینکه به این دو موضوع به طور جداگانه خواهیم پرداخت این است که فایل داده‌ها متفاوت از هم هستند، از آپشن‌های منو جداگانه در SPSS استفاده می‌کنند، و خروجی متفاوت از هم دارند. در نمونه‌های زیر نشان می‌دهیم که پس از ایجاد فایل داده‌ها چه اتفاقی رخ می‌دهد.

استفاده از آزمون t مستقل در SPSS

این خودآموز به شما می‌گوید که چگونه آزمون t مستقل را اجرا یا تفسیر کنید.

 مثال براساس مطالعۀ شوتلند و استراو (۱۹۷۶) می‌باشد. این افراد درصدد بودند تا تأثیر رابطۀ دریافتی بین نزاع یک زوج بر احتمال مداخلۀ شخص دیگر را کشف کنند.

برای آزمون این مسئله شرکت‌کنندگان به دو گروه تقسیم شدند و از آنها خواسته شد تا فیلم نزاع دو شخص را تماشا کنند.

فیلم‌ها به جز برای یک خط تعیین‌کننده مشابه هم بود. یک گروه فریاد زدن قربانی را می‌بیند که می گوید” تنهایم بگذار، تو را نمیشناسم”. در حالی که گروه دیگر همان شخص را می‌بیند که می‌گوید” تنهایم بگذار، نباید با تو ازدواج می‌کردم”.

از شرکت‌کنندگان خواسته شد تا میزان مداخلۀ خود را براساس مقیاس ۱-۵ ارزیابی کنند. داده‌ها را می‌توان به شرح زیر در فایل SPSS گنجاند:

“داده های هفته ۶ file.sav’: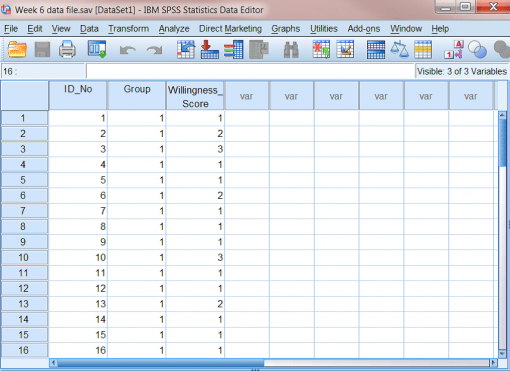

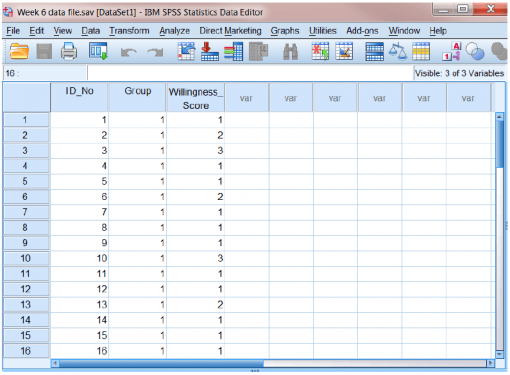
برای آزمون t مستقل، فایل داده ها باید دارای حداقل دو ستون باشد:

– یک ستون برای متغیر مستقل
– یک ستون برای متغیر وابسته

1. متغیر مستقل از کدها برای اختصاص دادن عضویت گروه به هر سطح یا وضعیت استفاده می کند. به عنوان مثال، از “۱” برای گروه کنترل و “۲” برای گروه آزمایشی می کند. هر ستون، متغیر متفاوتی را به نمایش می گذارد و هر ردیف حاوی داده های یک شرکت کننده است. ستون های مختلف داده های زیر را نشان می دهد
2. متغیر ID_No به شماره شناسۀ اختصاص یافته به هر شرکت کننده اشاره دارد. ما از اعداد به عنوان شناساگر به جای اسامی شرکت کنندگان استفاده می کنیم. این شیوه کمک می کند تا داده ها را بدون اینکه نام شرکت کنندگان فاش شود گردآوری کنیم. این شیوه در روانشناسی بویژه زمانی که گردآوردی داده ها با حاسیت زیاد مواجه است بسیار مفید و کاربردی است.

تعریف متغییر مستقل:

گروه متغیر به ما می گوید که شرکت کنندگان در چه وضعیت آزمایشی قرار دارند که به آن متغیر مستقل گفته می شود. IV برای آزمون t مستقل همیشه داده های مطلق (یا اسمی) است.

مثال :

ما از کد “۱” برای شرکت کنندگانی استفاده کردیم که زوج در حال نزاع را با هم غریبه در نظر گرفتند و کد “۲” برای کسانی که بین آنها رابطه ایی لحاظ کردند. در SPSS، به این کدها صفحۀ Variable View گفته می شود. برای آشنایی با این کدها به خودآموز اول با عنوان افزودن متغیرها مراجعه کنید.

Willingness_Score یک نوع رتبه بندی خودسنجی است که به این می پردازد که شرکت کنندگان تا چه اندازه مایل به مداخله در نزاعی که شاهدش هستند می باشند. این متغیر وابسته ما می باشد. در مثالی که بیان کردیم، این نمره یا اسکور با استفاده مقیاس ۵ امتیازی لیکرت رتبه بندی می شود که مقیاس بالاتر نشانگر احتمال بیشتر مداخله می باشد.

همانطور که در ابتدای خودآموز گفته شد، آزمون t مستقل، نمرات دو گروه را بر اساس یک متغیر خاص با هم مقایسه می کند.

• در این مورد، می خواهیم نمرات رضایت و میل دو گروه آزمایشی را با هم مقایسه کنیم.
  برای آغاز تحلیل، ابتدا بایدد روی منوی Analyze کلیک کنیم،
• گزینۀ Compare Means
• و سپس گزینۀ فرعی Independent-Samples T Test را انتخاب کنیم.

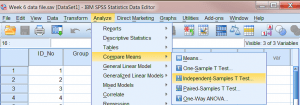
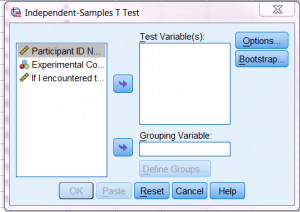
پس از آن کادر دیالوگ Independent Samples T-Test باز می شود.

در اینجا باید به SPSS بگوییم که قصد داریم کدارم متغیرها را تحلیل کنیم. شاید متوجه شوید که متغیرهای شما در حال حاضر در پنجرۀ چپ قرار دارند.

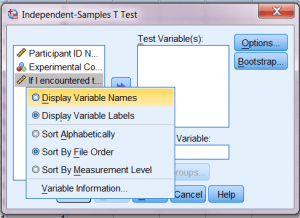
به محض اینکه Variable Labels(برچسب های متغیر) نمایش داده شد، به جز Variable Names (اسامی متغیر) کوتاهتر، خواندن بقیه دشوار است.

برای تغییر این وضعیت، با موس روی پنجره کلیک راست کنید و گزینۀ نمایش را به شرح زیر به ‘Display Variable Names’ تغییر دهید:

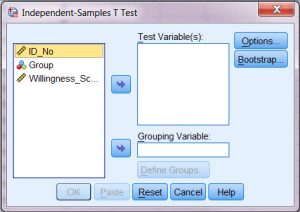
بدین ترتیب لیست متغیر تغییر می کند و خواندن آن راحت تر می شود.

اکنون می توانید کار تحلیل را شروع کنید. ابتدا، باید به SPSS بگوید که Grouping Variable (یا IV) شما چیست.

برای ای کار، متغیر Group را SELECT یا انتخاب کنید و سپس آن را با استفاده از پیکان آبی در قسمت پایین کنار کادر Grouping Variable به قاب پایینی سمت راست ببرید.

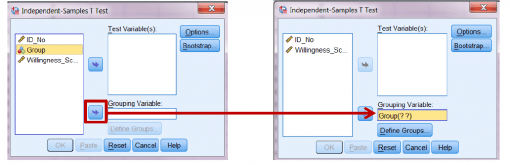
Groupاکنون دو علامت سئوال در کنار خود دارد. این به این معنی است که باید به SPSS بگویید کدام وضعیت ها را می خواهید مقایسه کنید.

همین که وضعیت های IV (دسته بندی های گروهی) با کدهای عددی وارد SPSS شد، باید به SPSS بگویید کدام کدها وضعیت هایی را که می خواهید مقایسه کنید نشان می دهد.

با کلیک روی دکمۀ Define Groups می توانید این کار را انجام دهید.

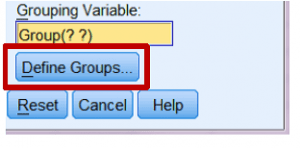
پس از این کادر دیالوگ Define Groups باز می شود و می توانید کدهای عددی را برای هر وضعیت آزمایشی که دارید مقایسه می کنید وارد کنید.

در این مورد، ما از “۱” برای کسانی که زوج را غریبه و از “۲” برای کسانی که زوج را دارای رابطه می دانستند استفاده می کنیم.

بدین ترتیب، باید اعداد ۱ و ۲ را به کادرهای ورودی Group 1 و Group 2 که در اینجا نشان داده می شود اضافه می کنیم.

بعد از آنکه هر دو عدد را وارد کردیم دکمۀ ادامه را باید فعال کنیم. برای ادامه روی continue کلیک کنید.

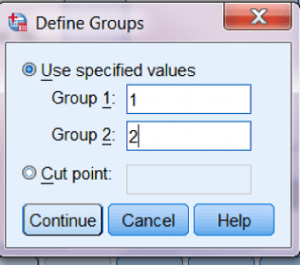
اکنون باید به SPSS بگویید می خواهید کدام متغیر وابسته را به تحلیل اضافه کنید.

برای این کار، Willingness_Score را انتخاب کنید

و روی دکمۀ پیکان بالایی کلیک کنید تا متغیر به پنجرۀ Test Variable(s) اضافه شود.

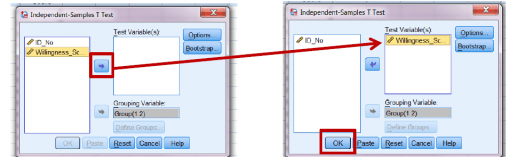
اکنون هر دو متغیر اضافه شده اند. برای اجرای تحلیل، روی OK کلیک کنید.

پنجرۀ خروجی به شما این امکان را می دهد که نتایج آزمون t را بررسی کنید: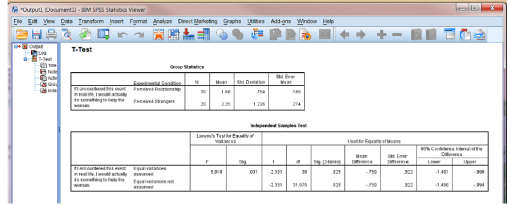

توجه داشته باشید که خروجی دارای دو قسمت است.

این دو قسمت موارد زیر را نشان می دهد:
۱) آمار توصیفی

۲) آمار استنتاجی

بهتر است نگاهی دقیق تر به کادرهای خروجی بیندازیم.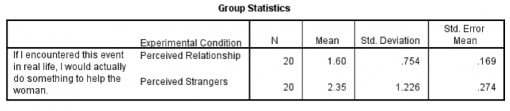

آمار گروهی

• کادر اول آمار توصیفی گروه ها را نشان می دهد. قبل از اینکه هر کار دیگری انجام دهید، بهتر است همیشه اول این کادر را بررسی کنید. با این کار می توانید به نگرش اولیه به طرح داده های خود دست یابید.
• در این جدول می توانید مشاهده کنید که میانگین نمره یا اسکور رضایت برای شرکت کنندگان در وضعیت رابطۀ دریافتی ۱٫۶۰ و در وضعیت غریبۀ دریافتی ۲٫۳۵ است. علاوه بر این، از انحراف معیار مشخصاست که تغییر داده ها (یعنی گسترش نمرات) برای گروه غریبه ها کمی (SD=1.23) بیشتر از گروه رابطه (SD=0.75) است.
  این شیوه ای استاندارد برای گزارش آمارهای توصیفی در شرایطی که می خواهید نتایج خود را گزارش دهید می باشد. در نتیجه، با نکاهی به میانگین های خود مشاهده می کنید که به طور متوسط شرکت کنندگانی که تصور می کردند زوج در حال نزاع با هم رابطه دارند احتمال اینکه تمایل به مداخله داشته باشند از شرکت کنندگان که زوج را با هم غیبه می دانستند کمتر بود.
  اما چگونه باید تفاوت بین میانگین ها را تفسیر کرد؟ برای پی بردن به اینکه آیا از لحاظ آماری تفاوتی بین نمرات وجود دارد ، در مرحله بعد باید نگاهی به جدول آمار استنتاجی بیندازید.
• 

آزمون نمونه های مستقل

این جدول آمار استنتاجی شما را نشان می دهد: خروجی آزمون t مستقل. نیازی نیست در خصوص تمام ستون های اینجا خود را نگران کنید( بسیاری از قسمت های جدول فقط برای سطح پیشرفته لازم است).

بخش های کلیدی جدول در قسمت بالا مشخص شده است و در قسمت زیر توضیح داده خواهد شد:

– آزمون لون برابری واریانس ها:

یکی از فرضیات آزمون t مستقل این است که دو گروهی که با هم مقایسه می کنید دارای پراکندگی نمرات مشابه هستند. (در غیراینصورت با عنوان همگنی یا برابری واریانس تلقی می شوند).

این ستون ها به ما می گویند که آیا مورد همین است یا نه.

چنانچه مقدار F معنی دار باشد، این وضعیت نشان می دهد که تفاوت های معنی دار آماری در شیول پراکندگی داده ها وجود دارد و با فرض همگنی مطابقت نداشته است.

توجه داشته باشید که جدول خروجی دارای دو ردیف است:

وقتی واریانس ها با هم برابر باشند از یکی استفاده می کنیم و وقتی برابر نباشند از ردیف دیگر استفاده می کنیم. در این نمونه، نمی توانیم واریانس ها را با هم برابر فرض کنیم. زیرا مقدار F معنی دار است (p = .031). بدین ترتیب، ما فقط باید مقادیر ردیف دوم جدول را بخوانیم.

آزمون t برابری میانگین ها:

در این ستون آمار آزمون t وجود دارد. این بخش به هفت بخش فرعی تقسیم می شود. اما فقط سه ستون در این مرحله مهم هستند. این سه ستون عبارتند از labelled t، df و sig (دنباله ای).
در این موقعیت شما تعیین می کنید که آیا فرضیۀ مورد آزمون تأیید شده است یا نه.
– مقدار t بدست آمده از t: این مقدار آمار آزمون t است که SPSS ماسبه کرده است. هر چه مقدار t بیشتر باشد، احتمال اینکه نتایج بصورت تصادفی رخ داده باشد کمتر است.

پیش از اینکه از کامپیوتر برای تحلیل داده ها استفاده شود، مقدار t به صورت دستی با استفاده از فرمول محاسبه می شد. مقدار به دست آمده سپس با مقدار بحرانی در جدولی به نام توزیع توزیع t مقایسه میشد. SPSS ما را از انجام همۀ این کارها معاف کرد.

 درجۀ ازادی df:

در اکثرآزمون های آماری با درجۀ ازادی مواجه خواهید شد. درجۀ آزادی مقداری است که از آن برای نمایش اندازۀ نمونه یا نمونه های مورد استفاده در یک آزمون آماری استفاده می شود و باید حتما گزارش شود.
شیوۀ گزارش درجۀ آزادی در ازمون های آماری مختلف متفاوت است. اما باید قبل از اینکه معنی داری نتیجه آزمون بررسی شود به دقت و درستی محاسبه گردد. زیاد نگران این مسئله نباشید. SPSS خود به بصورت خودکار مقدار آن را برایتان محاسبه می کند. اما باید توجه کنید که مقدار df با آزمون های مختلف tهمیشه نزدیک به تعداد کل شرکت کنندگان است.

Sig (دو دنباله ای):

میزان معنی داری (که به آن احتمال یا مقدار p) نیز می گویند در مورد این احتمال به ما می گوید که آیا نتایج بصورت تصادفی رخ داده است یا نه. در صورتی که این مقدار کمتر از .۰۵ باشد، فرضیه تأییدد می شود. در صورتی که بیشتر باشد، فرصیه بخاطر صفر یا خنثی بودن رد می شود که به معنی این است که هیچ تفاوتی بین دو گروه وجود ندارد.

در خصوص آزمون t مستقل،نرم‌افزار  SPSS  آزمون را در میزان معنی داری دو دنباله ای به صورت پیش فرض می سنجد. برای دستیابی به احتمال یک دنباله ای ( در صورتی که فرضیه یک جهتی باشد) مقدار p به نصف تقسیم می شود. در این موقعیت، می توانیم یک فرضیۀ یک دنباله ای مورد آزمون قرار دهیم مبنی بر اینکه افرادی که فکر می کردند بین زوج در حال نزاع رابطه ای وجود دارد احتمال اینکه در نزاع مداخله کنند از کسانی که خلاف این تصور می کردند کمتر خواهد بوداگر این کار را می کردیم، مقدار p 0.013 می شد (۱ دنباله ای).

برای بررسی خروجی به چه چیزی نیاز داریم؟
هنگامی که نتایج آزمون t را یادداشت می کنید، باید از طریق فرمول زیر مشخص کنید که آیا آزمون معنی دار بوده یا نه:
t (df) = t value, p = p value

در این فرمول اعداد مربوطه را در قسمت هایی که زیر آن خط کشیده شده وارد کنید. در مورد این مثال خاص، متوجه شدیم که آزمون t معنی دار است. ارزش p کمتر ۰٫۰۵ (p< .05) است.

t(31.58) = -2.33, p = 0.026

یافته ها چه چیزی به ما می گویند؟

زمانی که می‌خواهید یافته های خود را تفسیر و یادداشت کنید باید از اطلاعات هر دو آمار توصیفی و استنتاجی استفاده کنید. ترتیب ارائۀ این دو آمار اصلا مهم نیست. اما همیشه کار خود را با تفسیر واضح نتایج داده ها به پایان برسانید.

•  مرحلۀ اول: می توانید طرح داده های خود را با استفاده از میانگین و انحراف معیار اولین جدول خروجی توصیف کنید. در این مورد، می توانید به صورت زیر تفسیر خود را بنویسید:
  – نتایج نشان داد شرکت کنندگانی که متوجه رابطۀ بین زوج شدند نمرۀ تمایل کمتری (M=1.60, SD=.75) از کسانی که متوجه رابطه نشدند (M=2.35, SD=1.22) داشتند.
• مرحلۀ دو: از حروف و اعداد برای گزارش رسمی اختلاف معنی دار یا غیرمعنی دار استفاده کنید.
  آزمون t مستقل نشان داد که این طرح معنی دار است         t(31.58) = -2.33, p < 0.05.
•  مرحلۀ سه: در پایان، برای تفسیر و خلاصه سازی آنچه از فرضیه اتان متوجه شده اید باید این اطلاعات را در کنار هم قرار دهید. این مسئله را باید به انگلیسی(فارسی) سلیس بنویسید: مثال:
  روی هم رفته، این آزمون نشان می دهد که رابطۀ دریافتی بین قربانی و مرتکب بر تمایل شرکت کنندگان به مداخله تأثیر می گذارد و فرضیه را تأیید می کند.

اکنون شما یاد گرفته اید که چگونه با استفاده ازنرم افزار SPSS  آزمون T مستقل را انجام دهید.

09357258425 

www.pajuha.ir

[e-mail]

سفارش ترجمه تخصصی

آموزش آزمون دو جمله ای در spss

آزمون دو جمله‌ ای

فرض کنید یک جامعه آماری با داده‌های دو وضعیتی در اختیار دارید . به کمک آزمون دو جمله‌ای می‌توانیم به سوالاتی نظیر فهرست زیر در مورد این جامعه پاسخ دهیم.

• آیا می‌توان گفت که ۵۰٪ افراد جامعه، مرد هستند؟
• آیا، نسبت استفاده از وسایل حمل نقل عمومی در جامعه برابر با ۴۰٪ است؟
• آیا می‌توان گفت که نسبت مصرف کنندگان اینترنت همراه به تعداد کل سیمکارت کمتر از ۳۰٪ است.
• …

به تصویر زیر توجه کنید. به نظر می‌رسد که نمونه‌هایی از جامعه با متغیرهایی دو وضعیتی تهیه شده و قرار است براساس نمونه برای پارامتر نسبت گوی‌های قرمز و آبی دست به قضاوت بزنیم.

در این تصویر با سه جامعه مواجه هستیم. جامعه سمت راست، شامل پارامتر نسبت گوی‌های $$p=0.75$$ است و نمونه از همه آن‌ها تهیه شده است.

در جامعه دوم نسبت گوی‌های قرمز به آبی برابر با ۵۰٪ است و البته این قاعده در نمونه نیز دیده می‌شود.

در تصویر سمت چپ، نسبت گوی‌های قرمز به آبی ۲۵٪ است که البته در نمونه چنین چیزی دیده نمی‌شود در نتیجه ممکن است رای یا قضاوت ما در مورد این جامعه توسط نمونه آبی بودن همه اعضا باشد.

همانطور که دیده می‌شود ممکن است نمونه‌های مختلفی از هر جامعه تهیه شود. بنابراین سه شکل یا حالت مختلف (که با خطوط نارنجی مشخص شده‌اند) برای نمونه گرفته شده از جامعه سمت راست دیده می‌شود که هر کدام ممکن است برآورد متفاوتی از جامعه واقعی ارائه دهند. به این ترتیب وجود یک آزمون آماری که بتواند با دقت مناسب براساس یک نمونه در مورد پارامتر جامعه دید مناسبی به ما بدهد، ضروری است.

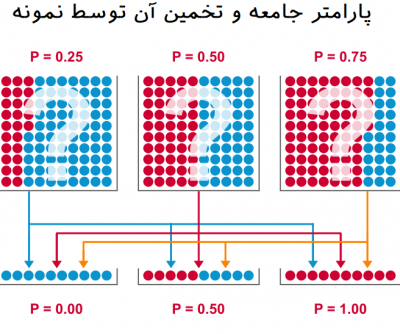متاسفانه ممکن است نمونه‌ها گواه یا معیاری خوبی برای تشخیص اطلاعات و پارامترهای واقعی جامعه نباشند. جالب است که این تصویر نشان می‌دهد، گاهی ممکن است براساس نمونه و انجام آزمون دچار خطا شده و به نادرستی نسبت را پیش‌بینی کنیم. البته می‌دانیم که این اشکال به خطای نمونه‌گیری یا به نوعی توان آزمون بستگی دارد.

اساس و پایه آزمون فرض آماری بر نمونه و توزیع آماره آزمون قرار گرفته است. به این ترتیب سعی داریم به کمک نمونه تصادفی در مورد خصوصیات جامعه آماری قضاوت کنیم. در آزمون فرض آماری، ابتدا حدس یا نظری در مورد پارامتر جامعه داریم، سپس با نمونه‌گیری و محاسبات مرتبط با آن، سعی داریم که این حدس یا فرضیه اولیه را مورد آزمایش یا آزمون قرار دهیم. این فرضیه را «فرض صفر» (Null Hypothesis) می‌نامیم.

ممکن است بعضی از مقدارهای حاصل از نمونه بسیار از فرض اولیه دور باشند در نتیجه نمی‌توانیم آن‌ها را تاییدی بر این فرض در نظر بگیریم در نتیجه آن فرض را رد می‌کنیم. ولی اگر نمونه بتواند فرضیه اولیه را مورد تایید قرار دهد، خواهیم گفت نمونه دلیلی برای رد فرض صفر ندارد ولی توجه داشته باشید که هرگز نمی‌توان گفت که فرض صفر صحیح است زیرا ممکن است یک نمونه دیگر، دلیلی بر رد فرض صفر ارائه کند.

با توجه به اینکه در آزمون دو جمله‌ای با متغیرهای دو وضعیتی مواجه هستیم، سوال اصلی در اینجا می‌تواند به این صورت نوشته شود: «آیا احتمال آنکه از بین ۱۰ نمونه تصادفی ۲ موفقیت حاصل شود، برابر با ۰٫۵ است؟»

برای پاسخ به این پرسش از آزمون دو جمله‌ای استفاده خواهیم کرد. ابتدا فرضیات و شرایط مربوط به این آزمون را مورد بررسی قرار می‌دهیم.

شرایط آزمون دو جمله‌ای

از آنجایی که این آزمون از نوع ناپارامتری است، وجود توزیع نرمال برای داده‌ها الزامی نیست. البته باید توجه داشت که در اینجا با داده‌های دو وضعیتی مواجه هستیم. بنابراین توزیع چنین داده‌هایی دو جمله‌ای خواهد بود.

البته ممکن است داده‌های حاصل از نمونه به صورت کمی باشند ولی با استفاده از یک نقطه برش می‌توانیم آن‌ها را به دو طبقه یا دو وضعیت تفکیک کنیم.

مثال:

• اگر بخواهیم آزمونی  که درصد افرادی که بازنشسته هستند (بالای ۶۰ سال سن دارند) آیا با ۳۰٪ برابر است با خیر. بگیریم .
• به این ترتیب یک متغیر کمی را بوسیله برش از مقدار ۶۰ به دو گروه بالای ۶۰ سال و زیر ۶۰ سال شکسته‌ایم.
• البته توجه داشته باشید که اگر مقدار احتمال در فرض صفر به صورت $$p=0.5$$ باشد، می‌توانیم از آزمون علامت نیز برای حل این مسئله استفاده کنیم.
• در این حالت به نظر می‌رسد که نقطه برش می‌تواند همان میانه در نظر گرفته شود زیرا ۵۰٪ داده‌ها از آن بزرگتر یا کوچکتر هستند.

مثال۲:

فرض کنید یک نمونه تصادفی از افراد جامعه تهیه کرده‌ایم. از هر یک از این افراد سنشان را پرسیده و ثبت کرده‌ایم. بنا به مقادیر حاصل از سن افراد متغیر جدیدی تعریف می‌کنیم که مقدار آن برای افرادی که بیش از ۶۰ سال سن دارند برابر با ۱ و در غیراینصورت برابر با ۰ است. به این ترتیب از روی متغیر کمی سن یک متغیر کیفی با دو وضعیت ایجاد کرده‌ایم که می‌تواند در آزمون علامت یا در آزمون دو جمله‌ای به کار رود.

اگر  متغیر تصادفی با توزیع دو جمله‌ای باشد، آنگاه شکل تابع احتمال آن به صورت زیر خواهد بود.

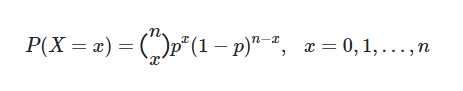
در این صورت می‌نویسیم ‌ است. هر یک از این پارامترها را در ادامه معرفی کرده‌ایم.

• تعداد نمونه در اینجا برابر با است.
• تعداد موفقیت‌ها در اینجا برابر با  است.
• احتمال موفقیت در هر بار آزمایش برنولی برای اعضای جامعه آماری ثابت و برابر با  است.

واضح است که منظور از تعداد ترکیبات  از  است. فرض کنید که  تعداد موفقیت در یک آزمایش دو جمله‌ای با ۱۰ نمونه و احتمال موفقیت  باشد. آنگاه نموداری که در تصویر زیر می‌بینید مقدار احتمال برای هر یک از تعداد موفقیت‌ها را نشان می‌دهد. مشخص است که این نمودار همان نمودار مربوط به تابع احتمال دو جمله‌ای است.

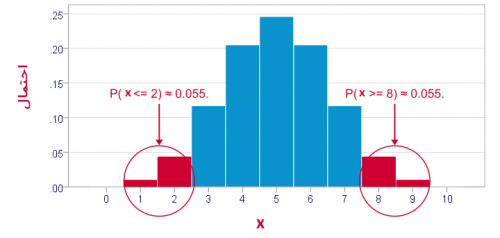
در نمودار بالا، مقدارهای بحرانی برای توزیع دو جمله‌ای را می‌بینید. بنابراین اگر  کمتر از ۲ یا بیشتر از ۸ باشد به نظر می‌رسد که احتمالات باید برابر با  باشد.

بنابراین اگر این میزان احتمال را برای یک نمونه تصادفی بزرگتر از این مقدار مشاهده کنیم، به نظر می‌رسد که باید مشاهدات از چنین توزیعی نباشند.

در چنین حالتی قاعده تصمیم به صورت  برای آزمون یکطرفه چپ و $$X>x$$ برای آزمون یکطرفه راست است.

بنابراین اگر مقدار احتمال هر یک از این حالت‌ها از مقدار خطای نوع اول کمتر باشد، فرض صفر در سطح آزمون  رد خواهد شد.

آزمون دو جمله‌ای در SPSS

در این نوشتار به منظور اجرای آزمون دو جمله‌ای، از نرم‌افزار SPSS استفاده کرده‌ایم. البته اگر می‌خواهید از نحوه اجرای این آزمون در زبان برنامه‌نویسی و محاسبات آماری R آگاه شوید بهتر است نوشتار آزمون علامت (Sign Test) — به زبان ساده را مطالعه کنید. به این ترتیب به نظر می‌رسد که می‌توان آزمون علامت را حالت خاصی از آزمون دو جمله‌ای در نظر گرفت.

نکته:

برای به کارگیری SPSS در حل مسائل مربوط به آزمون دو جمله‌ای بعنوان مثال:

فرض کنید  فایل حاوی اطلاعاتی در مورد عنکبوت‌های ماده و نر موجود می باشد و قرار است به واسطه پانزده نمونه تصادفی، نسبت عنکبوت‌های نر را در جامعه آماری عنکبوت‌های خانگی آزمون کنیم. طبق یک نظریه، ادعا شده است که این نسبت برابر با  است. از آنجایی که داده‌های مربوطه به صورت دو وضعیتی هستند، برای مشخص کردن نسبت یا احتمال موفقیت (مشاهده عنکبوت نر) از آزمون دو جمله‌ای استفاده خواهیم کرد. با سعی و تلاش فراوانی از گوشه گوشه‌های خانه تعداد ۱۵ عنکبوت جمع‌آوری و وضعیت جنسیت آن‌ها بررسی شده است. لازم به توضیح است که عنکبوت‌های ماده از نوع نر بزرگتر هستند.

به منظور شناخت از وضعیت و نسبت عنکبوت‌های درون نمونه بهتر است اطلاعاتی از وضعیت این داده‌ها ارائه کنیم.

جدول فراوانی و نمودار فراوانی می‌توانند به خوبی این کار را برایمان انجام دهند. کافی است از فهرست Analysis گزینه Descriptive Statistics و دستور Frequency را اجرا کنید.

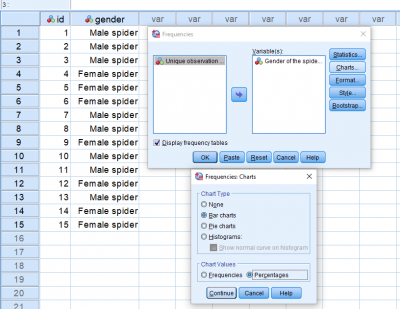همانطور که می‌بینید از نمودار Bar charts با مقدارهای درصدی Percentages استفاده شده است تا نمودار فراوانی به همراه برچسب مقدارها و فراوانی درصدی نمایش داده شود. البته برای اجرای این دستورات می‌توانید از کد زیر در پنجره Syntax نیز استفاده کنید.

 

خروجی این دستور به صورت زیر است. البته توجه داشته باشید برای نمایش تصویری فراوانی‌ها از نمودار میله‌ای استفاده کرده‌ایم به این ترتیب به نظر می‌رسد که درصد فراوانی برای عنکبوت‌های نر بیشتر از عنکبوت‌های ماده است. این ادعا توسط جدول فراوانی نیز تایید می‌شود. ولی نباید به همین جا اکتفا کنیم. شاید این اختلاف ناشی از نمونه بوده ولی در جامعه آماری چنین نباشد.

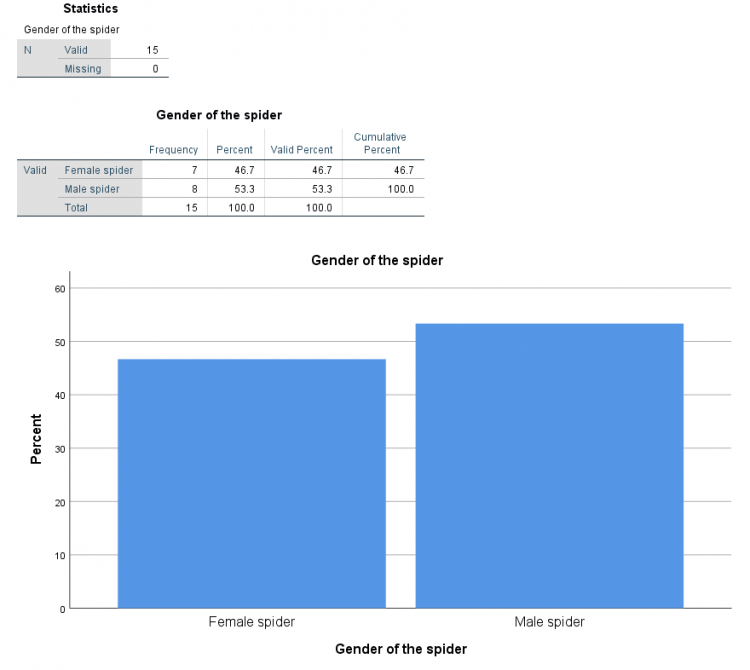بنابراین باید از یک آزمون آماری استفاده کنیم تا بتوانیم در مورد پارامتر جامعه قضاوت مناسب‌تری داشته باشیم. در اینجا با توجه به دو وضعیتی بودن مقدار متغیر، از آزمون دو جمله‌ای و توزیع دو جمله‌ای استفاده خواهیم کرد.

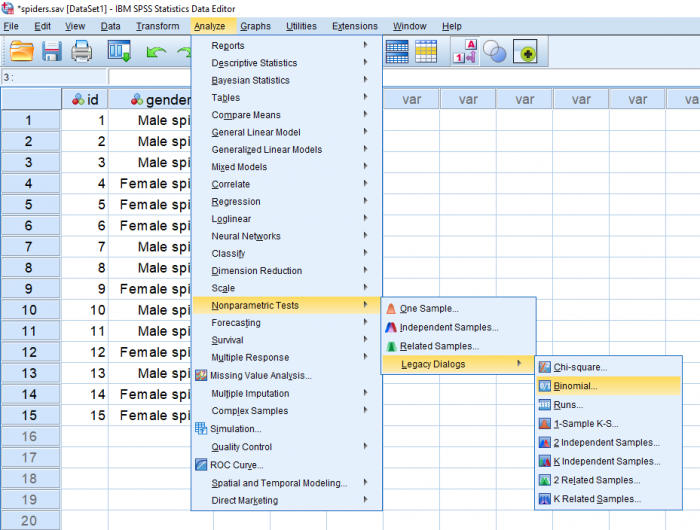
به منظور دسترسی به آزمون دوجمله‌ای در SPSS بهتر است مطابق تصویر بالا عمل کنید و از فهرست Analysis، گزینه Nonparametric Tests و انتخاب Legacy Dialogs و دستور Binomial را اجرا کنید. به این ترتیب پنجره مربوط به اجرای آزمون دوجمله‌ای مطابق باتصویر زیر ظاهر خواهد شد.

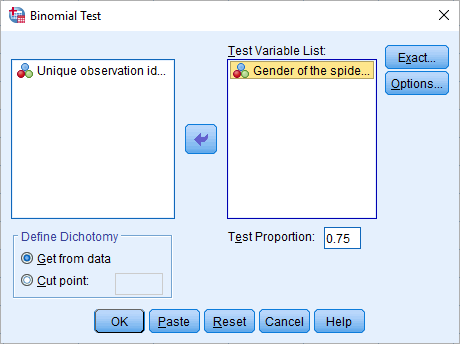همانطور که در تصویر بالا مشاهده می‌کنید، متغیر جنسیت عنکبوت‌ها در کادر Test Variable List قرار گرفته تا نشان دهد که آزمون باید برای این متغیر اجرا شود. در کادر test Proportion نیز مقداری که برای احتمال در فرض صفر در نظر گرفته شده، وارد می‌شود. با توجه به صورت مسئله این مقدار  ثبت شده است. به این ترتیب فرضیات مربوط به این مسئله در زیر دیده می‌شود.

اگر لازم است می‌توانید با استفاده از کادر Define Dichotomy مشخص کنید که متغیر معرفی شده دو مقداری است یا باید توسط یک نقطه برش به دو گروه تفکیک شود. برای این کار کافی است با انتخاب Cut point مقداری که محل برش را تعیین می‌کند، مشخص کنید.

نکته: اگر از پنجره Syntax و کد نویسی در SPSS استفاده می‌کنید، کافی است دستورات زیر را به کار برید.

با فشردن دکمه OK خروجی این آزمون به صورت زیر خواهد بود. مشخص است که با توجه به مقدار Sig و مقایسه آن با $$\alpha =\mathrm{۰٫۰۵}$$ فرض صفر را رد نخواهیم کرد زیرا به نظر می‌رسد که مقدار احتمال (Exact Sig) از احتمال خطای نوع اول () بیشتر است. پس نمونه دلیلی برای رد فرض صفر ارائه نکرده است.

نکته: باید توجه داشت که آزمون دو جمله‌ای، اولین مقدار در ستون متغیر را به عنوان موفقیت در نظر می‌گیرد. بنابراین از آنجایی که برای اولین مشاهده مقدار جنسیت برابر با ۱ یعنی عنکبوت نر ثبت شده، آزمون در مورد نسبت عنکبوت‌های نر خواهد بود.

در جدول Binomial Test مشخص است که در ستون Observed Prop برای مشاهده عنکبوت ماده حدود  و برای عنکبوت نر برابر با  است. فاصله مقدار  تا  باعث نشده است تا فرض صفر رد شود. در نتیجه اختلاف بین درصدها بین فرض صفر و نتیجه حاصل از نمونه، ناشی از خطای نمونه‌گیری است و این اختلاف در جامعه آماری وجود ندارد. به این معنی که درصد عنکبوت‌های نر در جامعه آماری همان نسبت  است. باز هم توجه داشته باشید که در پانوشته جدول Binomial Test مشخص شده که فرض مقابل به صورت $$<0.75$$ است در نتیجه آزمون یک طرفه خواهد بود.

حال در نظر بگیرید که قرار است آزمون را برای نسبت عنکبوت‌های ماده اجرا کنیم. کافی است هفت مشاهده اول را برای عنکبوت‌های ماده و هشت مشاهده بعدی را برای عنکبوت‌های نر در نظر بگیریم. به این ترتیب می‌توانیم با استفاده از وزن‌‌دهی به مشاهدات این اطلاعات را به طور خلاصه در SPSS‌ وارد کنیم. به تصویر زیر دقت کنید.

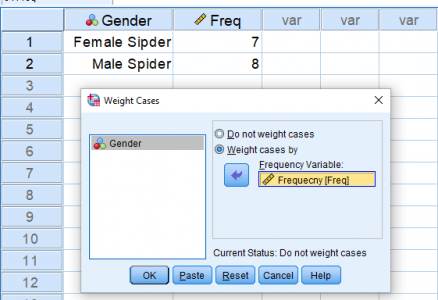با این کار فراوانی‌ها را در ستون Freq و مقدار را در ستون Gender‌ وارد کرده‌ایم. به این ترتیب مقدار ۰ که برای عنکبوت‌های ماده تعریف شده، هفت بار و مقدار ۱ که برای عنکبوت‌های نر در نظر گرفته شده، ۸ بار در آزمون دو جمله‌ای محسوب می‌شوند.

حال به اجرای آزمون دو جمله‌ای بر این اساس می‌پردازیم. مشخص است که با توجه به اینکه اولین مقدار مربوط به عنکبوت‌های ماده است، نسبت این گونه از عنکبوت‌ها در آزمون دو جمله‌ای مورد بررسی قرار می‌گیرد. نتیجه اجرا در این صورت مطابق با تصویر زیر است.

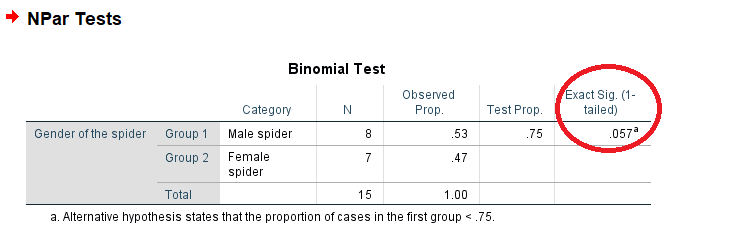با توجه به آزمون یکطرفه و مقدار Exact Sig که در ستون آخر جدول Binomial Test نوشته شده، در سطح خطای  فرض صفر رد می‌شود.

در نتیجه نمی‌توان درصد عنکبوت‌های ماده را برابر با  در نظر گرفت.

آنچه که گفته شد، مسیر دسترسی به دستور مستقیم آزمون دو جمله‌ای و شکل و شیوه تفسیر خروجی‌های آن بود.

شیوه جدید دسترسی مستقیم آزمون دو جمله ای:

می‌توانید گزینه One Sample را از گزینه Nonparametric Tests انتخاب کرده و تنظیمات را به شکلی در‌آورید که آزمون دو جمله‌ای اجرا شود. ابتدا لازم است که نوع آزمون را مشخص کنید. در تصویر زیر درخواست شده که آزمون توسط کاربر انتخاب شود زیرا گزینه Customize Analysis‌ فعال شده است.

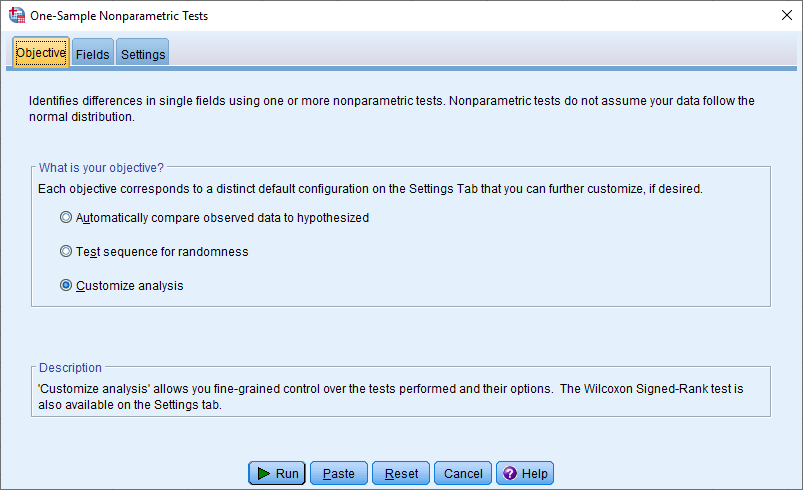
با انتخاب برگه Fields، متغیرهایی که باید در آزمون به کار گرفته شوند، تعیین می‌شود. البته ممکن است SPSS با توجه به نقشی که هر یک از متغیرها دارند، بطور خودکار این کار را انجام دهد. واضح است که متغیر Gender باید به عنوان متغیر مورد نظر انتخاب شود.

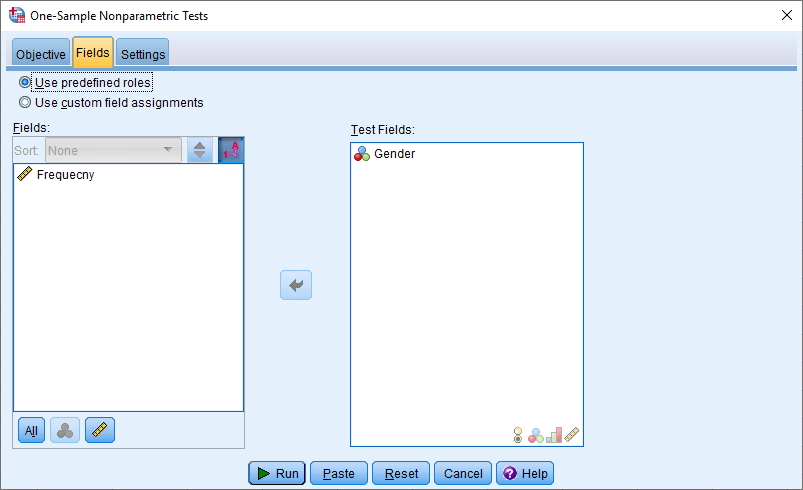
در بخش انتهایی نیز باید نوع آزمون و شیوه اجرای آن تنظیم شود. برگه Settings این وظیفه را به عهده دارد. بنابراین با انتخاب گزینه Customize tests و (Compare observed binary probability to hypothesized (binomial test نوع آزمون را دو جمله‌ای مشخص خواهید کرد.

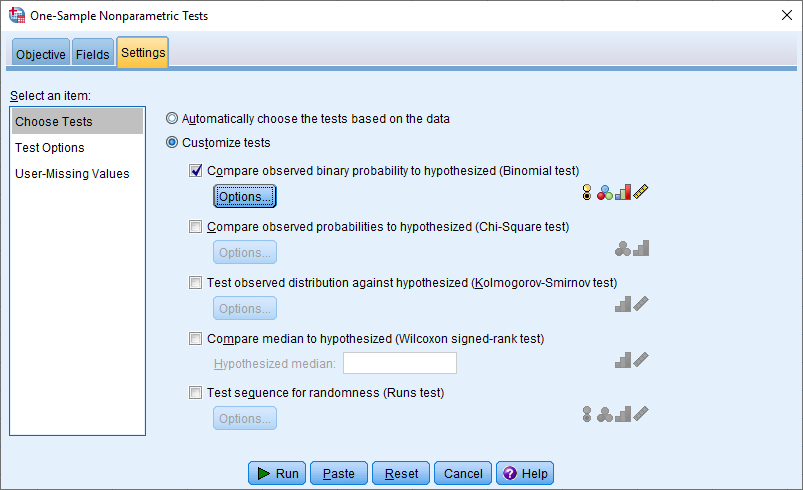
اگر لازم است تنظیماتی نظیر تعیین مقدار احتمال در فرض صفر یا انتخاب مقدار متغیر به عنوان مقدار موفقیت صورت بگیرید از دکمه Options مربوط به این آزمون استفاده کنید. برای پاسخ به مسئله مربوط به عنکبوت‌های ماده کافی است تنظیمات را مطابق با تصویر زیر تعیین کنید.

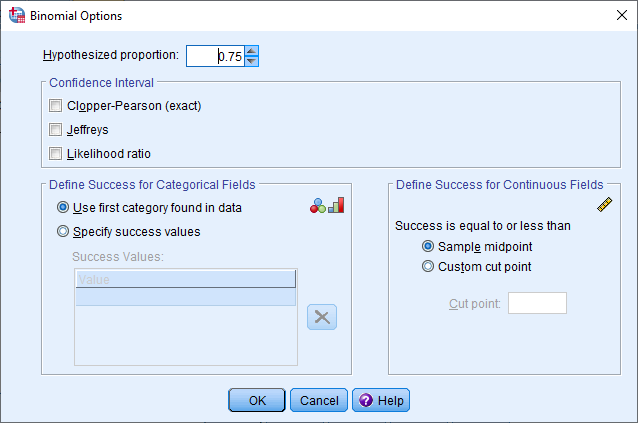با فشردن دکمه Run در پنجره اصلی، آزمون اجرا شده و نتایج مطابق با تصویر زیر ظاهر خواهند شد. البته توجه دارید که باید نتیجه‌ها مطابق با مثال قبل باشند.

خروجی‌هایی که توسط دستورات جدید در SPSS ایجاد می‌شوند، شامل اطلاعاتی بیشتری نیز هستند. همانطور که می‌بینید در ستون Decision مشخص است که فرض صفر در سطح خطای  رد می‌شود.

البته با توجه به ستون Sig این امر مطابق با خروجی‌های قبلی همین نتیجه را خواهد داد. اگر روی این جدول دوبار کلیک کنید، وارد صفحه‌ای می‌شوید که اطلاعات بیشتری در مورد آزمون و متغیرها در خود دارد. چنین پنجره‌هایی به Model Viewer معروف هستند. در تصویر زیر پنجره‌ Model Viewer برای آزمون دو جمله‌ای را می‌بینید

. سمت راست نمودارها و آماره‌های توصیفی و سمت چپ نیز نتیجه اجرای آزمون دو جمله‌ای دیده می‌شود.

09357258425 

www.pajuha.ir

[e-mail]

سفارش ترجمه تخصصی

سطح معنی داری آماری و خطاهای آماری در spss

تعریف آمار:

روش‌هائی برای جمع آوری، تنظیم و تجزیه و تحلیل اطلاعات عددی درباره یک موضوع مشخص که بصورت زیر می‌باشد.

– طرح نمونه گیری یا آزمایشات: آن دسته از علم آمار را گویند که با جمع‌آوری اطلاعات یا طرح آزمایشات سروکار دارد.

– آمار توصیفی: آن دسته از علم آمار را گویند که با دسته‌بندی و تلخیص دادها سروکار دارد.

– آمار استنباطی: آن دسته از علم آمار را گویند که باتجزیه و تحلیل و نتیجه گیری از داده‌ها سروکارر دارد.

۱٫ طرح نمونه گیری یا آزمایشات:

نمونه، بخشی از جامعه‌ی تحت بررسی است که با روشی از پیش تعین شده انتخاب می‌شود که می‌توان از این بخش، استنباط‌هایی درباره کل جامعه انجام داد.

به دلایل زیر از نمونه‌گیری به جای سرشماری کل جامعه استفاده می‌شود:

– کاهش هزینه

– افزایش سرعت کار

– بالا بودن توان کار

– بالا بودن میزان درستی کار

– پرهیز از خراب کردن واحد‌های جامعه

انواع روش‌های نمونه‌گیری: آموزش نرم افزار SPSS 

الف) روش احتمالی:

همه افراد جامعه از شانس مساوی برای انتخاب شدن برخوردارند. این روش جنبه علمی دارد.

ب) روش غیر احتمالی:

همه افراد شانس مساوی ندارند جنبه علمی هم ندارد. در پایان‌نامه استفاده نمی‌شود. مانند روش سهمیه‌بندی، اتفاقی، قضاوتی، هدفدار و غیره.

الف)روش احتمالی:

۱- تصادفی:

۱٫۱ – ساده: تعداد افراد را داریم ولی اطلاعات و مشخصات آنها را نداریم.

۲٫۱ – سیستماتیک: فرض کنید جامعه‌ای به حجم N تحت بررسی باشد و واحدهای جامعه را از ۱ تا N شماره گذاری کنند.

۲- خوشه‌ای: دراین روش، خوشه‌های جامعه را از ۱ تا N شماره‌گذاری و سپس n خوشه را به تصادف انتخاب می‌کنیم.

۲٫۱-یک مرحله‌ای: اگر مشخصه‌ی همه‌ی واحدهای موجود در این n خوشه را اندازه بگیریم، دنباله‌ای از اندازه ها بدست می‌آید که آن را نمونه گیری خوشه‌ای یک مرحله‌ای می‌نامیم.

۲٫۲- دو مرحله‌ای: اگر از هر n خوشه تعدادی انتخاب کنیم، آن را نمونه گیری خوشه‌ای دو مرحله‌ای می‌گویند.

۳- طبقه‌بندی شده: در نمونه گیری با طبقه‌بندی، طبقات الزاماً باید همگن باشند، اما چنین الزامی در اینجا نیست.طبقه‌بندی از نظر جنس، سن، سال، برند و غیره

روش‌های تعین حجم نمونه

۱- جدول مورگان: ساده تریین روش استفاده از جدول مورگان است

 تعریف سطح معنی دار در spss

قدم بعدی مشخص کردن درجه ای برای معنی دار بودن تفاوت ها و حجمی برای نمونه مورد بررسی است.

روش کار این است که فرض را به نفع فرض رد می کنیم به شرط اینکه از یک آزمون آماری مقداری به دست آوریم که احتمال وقوع آن مقدار با توجه به برابر یا کمتر از یک احتمال بسیار کوچک باشد، که با نشان داده می شود، باشد و به آن؛ «سطح معنی داری» (significance level) گفته می شود.

مقادیری که معمولا برای استفاده می شود اکثرا ۰٫۰۱ و۰٫۰۵ است.

از انجا که مقدار α در تعیین اینکه باید رد شود یا نه دخالت مستقیم دارد، الزام رعایت عینیت در تحقیق ایجاب می کند که را پیش از شروع جمع آوری داده ها مشخص کنیم.

سطح معنی داری که محقق برای تعیین در تحقیق α انتخاب می کند براساس تخمین او از اهمیت و یا درجۀ قابلیت کاربرد یافته هایش مبتنی است.

طبیعی است که اگر تحقیق مثلا درباره آثار درمانی عمل جراحی روی مغز باشد، محقق باید α را خیلی کمتر در نظر بگیرید زیرا خطرهای رد کردن نادرست فرضیه صفر بسیار زیاد است.

هنگام اتخاذ تصمیم دربارۀ H0 ممکن است دو نوع خطا پیش آید:

خطای نوع اول (Type I): رد کردن فرض H0 در حالی که درست است.

خطای نوع دوم (Type II): پذیرفتن فرض H0در حالی که غلط است.

احتمال وقوع خطای نوع اول با α ارتباط دارد، هر چهα بزرگتر شود، احتمال اینکه H0 را به غلط رد کنیم یا به عبارت دیگر، احتمال اینکه مرتکب خطای نوع اول شویم، افزایش می یابد.

خطای نوع دوم معمولا باβ نشان داده می شود.

حروف لاتینα و β هم برای نشان دادن «نوع خطاها» و هم «ارتکاب خطاها» به کار می روند، یعنی: (رد کردن H0 وقتی H0 درست است) P = (خطای نوع اول) P =α (رد نکردن H0 وقتی H0 غلط است ) P = (خطای نوع دوم) P=β احتمالα به مقدار مشخص پارامتر در دامنه ای بستگی داد که H0 آن را در بر می گیرد و حال آن که β به مقدار پارامتر در دامنه ای بستگی داد که H1آن را در بر می گیرد.

این خطاها و احتمال آن ها در رابطه با H0 را می توان به صورت جدول ۱-۴ خلاصه کد.

واضح است که بین α وβ رابطه معکوس وجود دارد. با بالا رفتنα مقدار β کاهش می یابد و برعکس.

این رابطه در آمار به «بده – بستان» (Trade off)بینα و β معروف است.

آن چه مسلم است، مجموعα وβ الزاما عدد یک نیست.

واضح است که در هر استنباط آماری، احتمال وقوع یکی از این دو نوع خطا وجود دارد و لازم است که آزمون کننده به نوعی سازش که تعادل بین احتمال وقوع این دو نوع خطا را به حد مطلوب برساند دست یابد.

آزمون های آماری مختلف، احتمال تعادل های مختلفی را عرضه می کنند.

در رسیدن به چنین تعادلی است که موضوع «توان آزمون» (Power Function) مطرح می شود.

توان آزمون عبارت است از احتمال رد H0 وقتی که H0 حقیقتا نادرست است: β-۱ = (احتمال وقوع خطای نوع دوم) – ۱ = توان آزمون آن چه موجب کاهش «خطای نوع اول»، « خطای نوع دوم» و همچنین «توان آزمون» می شود، افزایش حجم نمونه است.

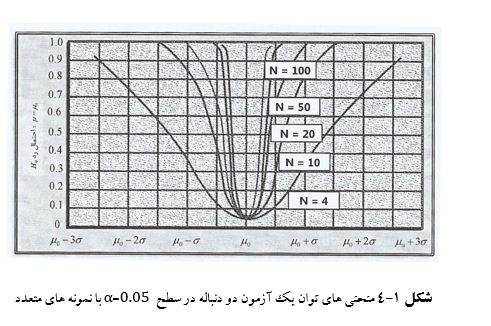
منحنی های شکل ۱-۴ نشان می دهد که وقتی حجم نمونه (n) افزایش می یابد احتمال وقوع خطای نوع دوم (β)کاهش می یابد.

در اینجا افزایش «توان آزمون» دو طرفۀ میانگین وقتی حجم نمونه افزایش می یابد با هم مقایسه شده است.

مشاهده می شود که وقتی حجم نمونه از ۴ به ۵۰٫۲۰٫۱۰ و۱۰۰ افزایش می یابد، چگونه توان آزمون نیز زیادتر می شود.

09357258425 

www.pajuha.ir

[e-mail]

سفارش ترجمه تخصصی

آموزش نحوه نرمال سازی داده ها در spss

آموزش گام به گام نحوه نرمال کردن داده ها در spss

در انجام بسیاری از تحلیل های آماری،توزیع نرمال نقش اساسی ایفا می کند در این روش ها به بررسی نرمال نرمال کردن یا همان نرمالیزه کردن داده ها در اس پی اس اس  می پردازیم و کمی زمان بر تر از سایر دستورات گفته شده این نرم افزار می باشد.

هدف از استانداردسازی داده‌ها چیست؟

این سؤال خیلی از هموطنان است که می پرسند استانداردسازی داده‌ها چه فایده ای دارد؟

پاسخ این است که استانداردسازی داده‌ها کمک می‌کند که اهمیت آن‌ها به واحد اندازه‌گیری‌شان بستگی نداشته باشد. در نتیجه در مواردی مانند داده‌کاوی و تحلیل داده‌های چند متغیره از داده‌های استاندارد شده استفاده می‌شود. همچنین استاندارد‌سازی برای داده‌های کمی و کیفی قابل اجرا است و چند روش استانداردسازی وجود دارد.

روش‏ های مختلف نرمال سازی داده

در بسیاری از روشهای آماری نرمال بودن متغیر وابسته یکی از فروض  اصلی  بشمار میرود که زیر به برخی روشهای معمول نرمال سازی اشاره شده است.
۱- وارون سازی  داده ها:  وارون کردن همه مشاهدات :  در صورت عدم مشاهده صفر
۲-  لگاریتم(LOG): محاسبه لگاریتم  همه مشاهدات :  در صورت منفی نبودن  مشاهدات
۳- ریشه دوم:  محاسبه ریشه دوم همه مشاهدات:  در صورت منفی نبودن مشاهدات
۴- تبدیل جانسون(Johnson Transformation) : سیستم  تبدیل جانسون بر مبنای سه توزیع  Bounded system(SB)  و Log-normal system (SL) و  Unbounded system (SU) و برآورد پارامترهای تورزیع های فوق  عمل میکند.

بهینه سازی پارامترهای توزیع  تا جایی که یکی از توابع تبدیل، بهترین  توزیع نرمال را تولید کند ادامه  می یابد. الگوریتم  انتخاب بهترین توزیع توسط  Polansky ,  Chou  در سال ۱۹۹۹معرفی شد. این روش با توجه به علامت جبری داد ه ها روشی مناسب برای نرمال سازی به شمار میرود.

۵- تبدیل باکس کاکس(Box-Cox transformation): این تبدیل یکی از روشهای قدرتمند در نرمال سازی توزیع مشاهدات به شمار میرود. این روش مقداری به عنون توان (λ) تعیین کرده و همه مشاهدات را به توان آنمیرساند و سپس ازمون نرمال روی مشاهدات انجام شده تا بهترین سری از مشاهدات بدست آید.مقدار λ بین –۵ تا ۵ تغییر میکند.این روش فقط برای داده های مثبت به کار میرود و این تنها نقطه ضعف این روش است.

آموزش مرحله به مرحله نرمال سازی داده ها در spss:

مرحله۱- داده ها را وارد محیط نرم افزار spss می کنیم. در این مرحله می توان داده ها را به صورت دستی وارد کرد و یا از محیط دیگری مثل اکسل داده ها را کپی کرد.

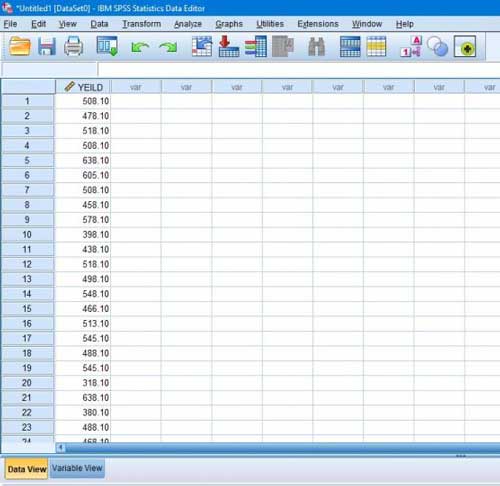مرحله۲- پس از اینکه داده ها را وارد کردید به تب Analyze رفته و وارد قسمت Descriptive Statistics و Explore شوید.

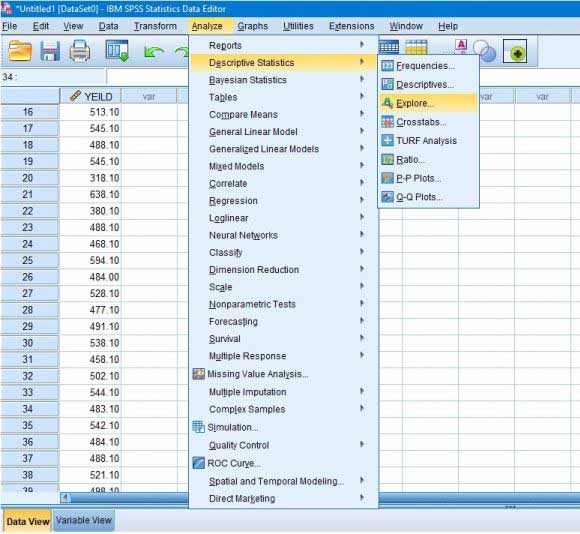مرحله۳- در پنجره باز شده، صفت مورد نظر را وارد کادر Dependent List می کنیم. در این مرحله اگر چند صفت داشته باشیم می توانیم آزمون نرمال بودن را به صورت همزمان روی همه صفات انجام دهیم بنابراین همه صفات را وارد کادر Dependent List می کنیم.

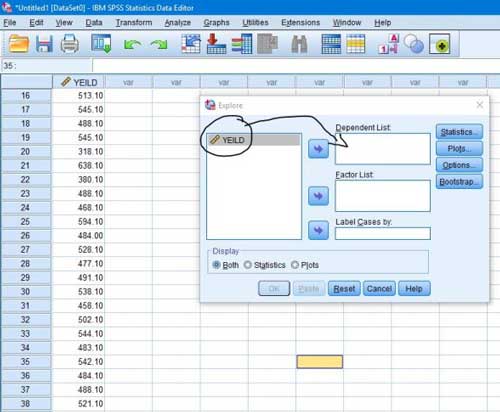مرحله۴- پس از وارد کردن صفات باید از قسمت Plots تیک عبارت Normality plots with tests را فعال و روی دکمه Continue و Ok کلیک می کنیم تا نتایج آزمون در پنجره Output ظاهر شود.

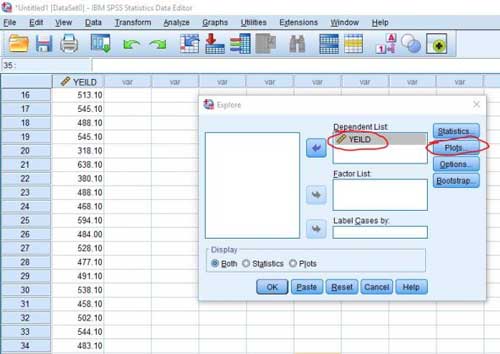
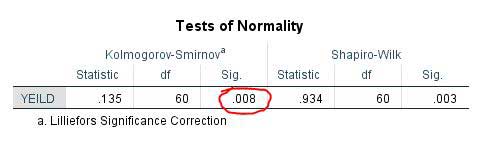
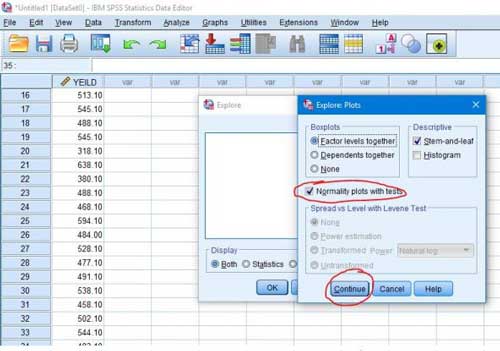مرحله ۵- مشاهده کردید که چگونه براحتی با دو آزمون، نرمال بودن داده ها بررسی شد. اکنون طبق گفته های بالا، نتایج آزمون کولموگروف-اسمیرنوف را بررسی می کنیم. در این جدول اگر مقدار sig. بیشتر از ۰٫۰۱ باشد داده ها نرمال و اگر کمتر از ۰٫۰۱ باشد داده ها توزیع نرمال ندارند و باید آنها را قبل از تجزیه واریانس تبدیل بکنیم.

09357258425 

www.pajuha.ir

[e-mail]

سفارش ترجمه تخصصی