سطح معنی داری آماری و خطاهای آماری در spss

تعریف آمار:

روش‌هائی برای جمع آوری، تنظیم و تجزیه و تحلیل اطلاعات عددی درباره یک موضوع مشخص که بصورت زیر می‌باشد.

– طرح نمونه گیری یا آزمایشات: آن دسته از علم آمار را گویند که با جمع‌آوری اطلاعات یا طرح آزمایشات سروکار دارد.

– آمار توصیفی: آن دسته از علم آمار را گویند که با دسته‌بندی و تلخیص دادها سروکار دارد.

– آمار استنباطی: آن دسته از علم آمار را گویند که باتجزیه و تحلیل و نتیجه گیری از داده‌ها سروکارر دارد.

۱٫ طرح نمونه گیری یا آزمایشات:

نمونه، بخشی از جامعه‌ی تحت بررسی است که با روشی از پیش تعین شده انتخاب می‌شود که می‌توان از این بخش، استنباط‌هایی درباره کل جامعه انجام داد.

به دلایل زیر از نمونه‌گیری به جای سرشماری کل جامعه استفاده می‌شود:

– کاهش هزینه

– افزایش سرعت کار

– بالا بودن توان کار

– بالا بودن میزان درستی کار

– پرهیز از خراب کردن واحد‌های جامعه

انواع روش‌های نمونه‌گیری: آموزش نرم افزار SPSS 

الف) روش احتمالی:

همه افراد جامعه از شانس مساوی برای انتخاب شدن برخوردارند. این روش جنبه علمی دارد.

ب) روش غیر احتمالی:

همه افراد شانس مساوی ندارند جنبه علمی هم ندارد. در پایان‌نامه استفاده نمی‌شود. مانند روش سهمیه‌بندی، اتفاقی، قضاوتی، هدفدار و غیره.

الف)روش احتمالی:

۱- تصادفی:

۱٫۱ – ساده: تعداد افراد را داریم ولی اطلاعات و مشخصات آنها را نداریم.

۲٫۱ – سیستماتیک: فرض کنید جامعه‌ای به حجم N تحت بررسی باشد و واحدهای جامعه را از ۱ تا N شماره گذاری کنند.

۲- خوشه‌ای: دراین روش، خوشه‌های جامعه را از ۱ تا N شماره‌گذاری و سپس n خوشه را به تصادف انتخاب می‌کنیم.

۲٫۱-یک مرحله‌ای: اگر مشخصه‌ی همه‌ی واحدهای موجود در این n خوشه را اندازه بگیریم، دنباله‌ای از اندازه ها بدست می‌آید که آن را نمونه گیری خوشه‌ای یک مرحله‌ای می‌نامیم.

۲٫۲- دو مرحله‌ای: اگر از هر n خوشه تعدادی انتخاب کنیم، آن را نمونه گیری خوشه‌ای دو مرحله‌ای می‌گویند.

۳- طبقه‌بندی شده: در نمونه گیری با طبقه‌بندی، طبقات الزاماً باید همگن باشند، اما چنین الزامی در اینجا نیست.طبقه‌بندی از نظر جنس، سن، سال، برند و غیره

روش‌های تعین حجم نمونه

۱- جدول مورگان: ساده تریین روش استفاده از جدول مورگان است

 تعریف سطح معنی دار در spss

قدم بعدی مشخص کردن درجه ای برای معنی دار بودن تفاوت ها و حجمی برای نمونه مورد بررسی است.

روش کار این است که فرض را به نفع فرض رد می کنیم به شرط اینکه از یک آزمون آماری مقداری به دست آوریم که احتمال وقوع آن مقدار با توجه به برابر یا کمتر از یک احتمال بسیار کوچک باشد، که با نشان داده می شود، باشد و به آن؛ «سطح معنی داری» (significance level) گفته می شود.

مقادیری که معمولا برای استفاده می شود اکثرا ۰٫۰۱ و۰٫۰۵ است.

از انجا که مقدار α در تعیین اینکه باید رد شود یا نه دخالت مستقیم دارد، الزام رعایت عینیت در تحقیق ایجاب می کند که را پیش از شروع جمع آوری داده ها مشخص کنیم.

سطح معنی داری که محقق برای تعیین در تحقیق α انتخاب می کند براساس تخمین او از اهمیت و یا درجۀ قابلیت کاربرد یافته هایش مبتنی است.

طبیعی است که اگر تحقیق مثلا درباره آثار درمانی عمل جراحی روی مغز باشد، محقق باید α را خیلی کمتر در نظر بگیرید زیرا خطرهای رد کردن نادرست فرضیه صفر بسیار زیاد است.

هنگام اتخاذ تصمیم دربارۀ H0 ممکن است دو نوع خطا پیش آید:

خطای نوع اول (Type I): رد کردن فرض H0 در حالی که درست است.

خطای نوع دوم (Type II): پذیرفتن فرض H0در حالی که غلط است.

احتمال وقوع خطای نوع اول با α ارتباط دارد، هر چهα بزرگتر شود، احتمال اینکه H0 را به غلط رد کنیم یا به عبارت دیگر، احتمال اینکه مرتکب خطای نوع اول شویم، افزایش می یابد.

خطای نوع دوم معمولا باβ نشان داده می شود.

حروف لاتینα و β هم برای نشان دادن «نوع خطاها» و هم «ارتکاب خطاها» به کار می روند، یعنی: (رد کردن H0 وقتی H0 درست است) P = (خطای نوع اول) P =α (رد نکردن H0 وقتی H0 غلط است ) P = (خطای نوع دوم) P=β احتمالα به مقدار مشخص پارامتر در دامنه ای بستگی داد که H0 آن را در بر می گیرد و حال آن که β به مقدار پارامتر در دامنه ای بستگی داد که H1آن را در بر می گیرد.

این خطاها و احتمال آن ها در رابطه با H0 را می توان به صورت جدول ۱-۴ خلاصه کد.

واضح است که بین α وβ رابطه معکوس وجود دارد. با بالا رفتنα مقدار β کاهش می یابد و برعکس.

این رابطه در آمار به «بده – بستان» (Trade off)بینα و β معروف است.

آن چه مسلم است، مجموعα وβ الزاما عدد یک نیست.

واضح است که در هر استنباط آماری، احتمال وقوع یکی از این دو نوع خطا وجود دارد و لازم است که آزمون کننده به نوعی سازش که تعادل بین احتمال وقوع این دو نوع خطا را به حد مطلوب برساند دست یابد.

آزمون های آماری مختلف، احتمال تعادل های مختلفی را عرضه می کنند.

در رسیدن به چنین تعادلی است که موضوع «توان آزمون» (Power Function) مطرح می شود.

توان آزمون عبارت است از احتمال رد H0 وقتی که H0 حقیقتا نادرست است: β-۱ = (احتمال وقوع خطای نوع دوم) – ۱ = توان آزمون آن چه موجب کاهش «خطای نوع اول»، « خطای نوع دوم» و همچنین «توان آزمون» می شود، افزایش حجم نمونه است.

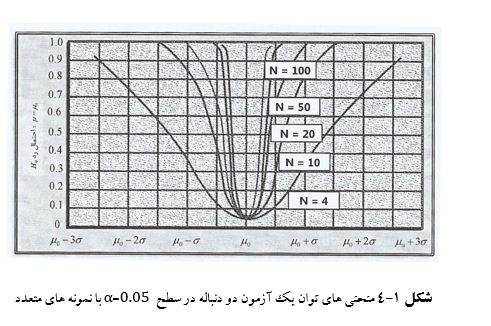
منحنی های شکل ۱-۴ نشان می دهد که وقتی حجم نمونه (n) افزایش می یابد احتمال وقوع خطای نوع دوم (β)کاهش می یابد.

در اینجا افزایش «توان آزمون» دو طرفۀ میانگین وقتی حجم نمونه افزایش می یابد با هم مقایسه شده است.

مشاهده می شود که وقتی حجم نمونه از ۴ به ۵۰٫۲۰٫۱۰ و۱۰۰ افزایش می یابد، چگونه توان آزمون نیز زیادتر می شود.

09357258425 

www.pajuha.ir

[e-mail]

سفارش ترجمه تخصصی