آموزش آزمون دو جمله ای در spss

آزمون دو جمله‌ ای

فرض کنید یک جامعه آماری با داده‌های دو وضعیتی در اختیار دارید . به کمک آزمون دو جمله‌ای می‌توانیم به سوالاتی نظیر فهرست زیر در مورد این جامعه پاسخ دهیم.

آیا می‌توان گفت که ۵۰٪ افراد جامعه، مرد هستند؟
آیا، نسبت استفاده از وسایل حمل نقل عمومی در جامعه برابر با ۴۰٪ است؟
آیا می‌توان گفت که نسبت مصرف کنندگان اینترنت همراه به تعداد کل سیمکارت کمتر از ۳۰٪ است.
…

به تصویر زیر توجه کنید. به نظر می‌رسد که نمونه‌هایی از جامعه با متغیرهایی دو وضعیتی تهیه شده و قرار است براساس نمونه برای پارامتر نسبت گوی‌های قرمز و آبی دست به قضاوت بزنیم.

در این تصویر با سه جامعه مواجه هستیم. جامعه سمت راست، شامل پارامتر نسبت گوی‌های $p = 0.75 " style="box-sizing: border-box; -webkit-tap-highlight-color: transparent; display: inline-block; line-height: 0; text-align: center; overflow-wrap: normal; word-spacing: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; margin: 0px; padding: 1px 0px; position: relative; font-family: IRANSans !important; font-size: 17px !important;"> p = 0.75$ است و نمونه از همه آن‌ها تهیه شده است.

در جامعه دوم نسبت گوی‌های قرمز به آبی برابر با ۵۰٪ است و البته این قاعده در نمونه نیز دیده می‌شود.

در تصویر سمت چپ، نسبت گوی‌های قرمز به آبی ۲۵٪ است که البته در نمونه چنین چیزی دیده نمی‌شود در نتیجه ممکن است رای یا قضاوت ما در مورد این جامعه توسط نمونه آبی بودن همه اعضا باشد.

همانطور که دیده می‌شود ممکن است نمونه‌های مختلفی از هر جامعه تهیه شود. بنابراین سه شکل یا حالت مختلف (که با خطوط نارنجی مشخص شده‌اند) برای نمونه گرفته شده از جامعه سمت راست دیده می‌شود که هر کدام ممکن است برآورد متفاوتی از جامعه واقعی ارائه دهند. به این ترتیب وجود یک آزمون آماری که بتواند با دقت مناسب براساس یک نمونه در مورد پارامتر جامعه دید مناسبی به ما بدهد، ضروری است.

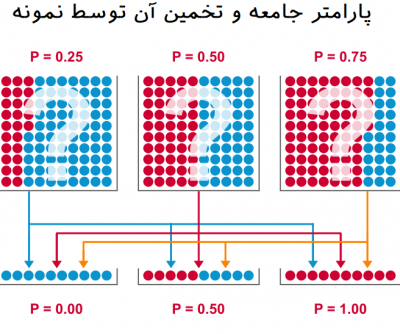متاسفانه ممکن است نمونه‌ها گواه یا معیاری خوبی برای تشخیص اطلاعات و پارامترهای واقعی جامعه نباشند. جالب است که این تصویر نشان می‌دهد، گاهی ممکن است براساس نمونه و انجام آزمون دچار خطا شده و به نادرستی نسبت را پیش‌بینی کنیم. البته می‌دانیم که این اشکال به خطای نمونه‌گیری یا به نوعی توان آزمون بستگی دارد.

اساس و پایه آزمون فرض آماری بر نمونه و توزیع آماره آزمون قرار گرفته است. به این ترتیب سعی داریم به کمک نمونه تصادفی در مورد خصوصیات جامعه آماری قضاوت کنیم. در آزمون فرض آماری، ابتدا حدس یا نظری در مورد پارامتر جامعه داریم، سپس با نمونه‌گیری و محاسبات مرتبط با آن، سعی داریم که این حدس یا فرضیه اولیه را مورد آزمایش یا آزمون قرار دهیم. این فرضیه را «فرض صفر» (Null Hypothesis) می‌نامیم.

ممکن است بعضی از مقدارهای حاصل از نمونه بسیار از فرض اولیه دور باشند در نتیجه نمی‌توانیم آن‌ها را تاییدی بر این فرض در نظر بگیریم در نتیجه آن فرض را رد می‌کنیم. ولی اگر نمونه بتواند فرضیه اولیه را مورد تایید قرار دهد، خواهیم گفت نمونه دلیلی برای رد فرض صفر ندارد ولی توجه داشته باشید که هرگز نمی‌توان گفت که فرض صفر صحیح است زیرا ممکن است یک نمونه دیگر، دلیلی بر رد فرض صفر ارائه کند.

با توجه به اینکه در آزمون دو جمله‌ای با متغیرهای دو وضعیتی مواجه هستیم، سوال اصلی در اینجا می‌تواند به این صورت نوشته شود: «آیا احتمال آنکه از بین ۱۰ نمونه تصادفی ۲ موفقیت حاصل شود، برابر با ۰٫۵ است؟»

برای پاسخ به این پرسش از آزمون دو جمله‌ای استفاده خواهیم کرد. ابتدا فرضیات و شرایط مربوط به این آزمون را مورد بررسی قرار می‌دهیم.

شرایط آزمون دو جمله‌ای

از آنجایی که این آزمون از نوع ناپارامتری است، وجود توزیع نرمال برای داده‌ها الزامی نیست. البته باید توجه داشت که در اینجا با داده‌های دو وضعیتی مواجه هستیم. بنابراین توزیع چنین داده‌هایی دو جمله‌ای خواهد بود.

البته ممکن است داده‌های حاصل از نمونه به صورت کمی باشند ولی با استفاده از یک نقطه برش می‌توانیم آن‌ها را به دو طبقه یا دو وضعیت تفکیک کنیم.

مثال:

اگر بخواهیم آزمونی که درصد افرادی که بازنشسته هستند (بالای ۶۰ سال سن دارند) آیا با ۳۰٪ برابر است با خیر. بگیریم .
به این ترتیب یک متغیر کمی را بوسیله برش از مقدار ۶۰ به دو گروه بالای ۶۰ سال و زیر ۶۰ سال شکسته‌ایم.
البته توجه داشته باشید که اگر مقدار احتمال در فرض صفر به صورت $p = 0.5 " style="box-sizing: border-box; -webkit-tap-highlight-color: transparent; display: inline-block; line-height: 0; text-align: center; overflow-wrap: normal; word-spacing: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; margin: 0px; padding: 1px 0px; position: relative; font-family: IRANSans !important; font-size: 17px !important;"> p = 0.5$ باشد، می‌توانیم از آزمون علامت نیز برای حل این مسئله استفاده کنیم.
در این حالت به نظر می‌رسد که نقطه برش می‌تواند همان میانه در نظر گرفته شود زیرا ۵۰٪ داده‌ها از آن بزرگتر یا کوچکتر هستند.

مثال۲:

فرض کنید یک نمونه تصادفی از افراد جامعه تهیه کرده‌ایم. از هر یک از این افراد سنشان را پرسیده و ثبت کرده‌ایم. بنا به مقادیر حاصل از سن افراد متغیر جدیدی تعریف می‌کنیم که مقدار آن برای افرادی که بیش از ۶۰ سال سن دارند برابر با ۱ و در غیراینصورت برابر با ۰ است. به این ترتیب از روی متغیر کمی سن یک متغیر کیفی با دو وضعیت ایجاد کرده‌ایم که می‌تواند در آزمون علامت یا در آزمون دو جمله‌ای به کار رود.

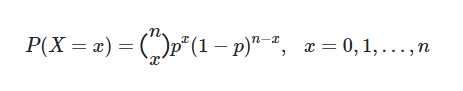
اگر $X " style="box-sizing: border-box; -webkit-tap-highlight-color: transparent; display: inline-block; line-height: 0; text-align: center; overflow-wrap: normal; word-spacing: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; margin: 0px; padding: 1px 0px; position: relative; font-family: IRANSans !important; font-size: 17px !important;"> X$ متغیر تصادفی با توزیع دو جمله‌ای باشد، آنگاه شکل تابع احتمال آن به صورت زیر خواهد بود.

در این صورت می‌نویسیم $X \sim B (n, p) " style="box-sizing: border-box; -webkit-tap-highlight-color: transparent; display: inline-block; line-height: 0; text-align: center; overflow-wrap: normal; word-spacing: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; margin: 0px; padding: 1px 0px; position: relative; font-family: IRANSans !important; font-size: 17px !important;">$ ‌ است. هر یک از این پارامترها را در ادامه معرفی کرده‌ایم.

تعداد نمونه در اینجا برابر با $n " style="box-sizing: border-box; -webkit-tap-highlight-color: transparent; display: inline-block; line-height: 0; text-align: center; overflow-wrap: normal; word-spacing: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; margin: 0px; padding: 1px 0px; position: relative; font-family: IRANSans !important; font-size: 17px !important;">$ است.
تعداد موفقیت‌ها در اینجا برابر با $x " style="box-sizing: border-box; -webkit-tap-highlight-color: transparent; display: inline-block; line-height: 0; text-align: center; overflow-wrap: normal; word-spacing: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; margin: 0px; padding: 1px 0px; position: relative; font-family: IRANSans !important; font-size: 17px !important;"> x$ است.
احتمال موفقیت در هر بار آزمایش برنولی برای اعضای جامعه آماری ثابت و برابر با $p " style="box-sizing: border-box; -webkit-tap-highlight-color: transparent; display: inline-block; line-height: 0; text-align: center; overflow-wrap: normal; word-spacing: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; margin: 0px; padding: 1px 0px; position: relative; font-family: IRANSans !important; font-size: 17px !important;"> p$ است.

واضح است که منظور از تعداد ترکیبات $x " style="box-sizing: border-box; -webkit-tap-highlight-color: transparent; display: inline-block; line-height: 0; text-align: center; overflow-wrap: normal; word-spacing: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; margin: 0px; padding: 1px 0px; position: relative; font-family: IRANSans !important; font-size: 17px !important;">$ از $n " style="box-sizing: border-box; -webkit-tap-highlight-color: transparent; display: inline-block; line-height: 0; text-align: center; overflow-wrap: normal; word-spacing: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; margin: 0px; padding: 1px 0px; position: relative; font-family: IRANSans !important; font-size: 17px !important;"> n$ است. فرض کنید که $X " style="box-sizing: border-box; -webkit-tap-highlight-color: transparent; display: inline-block; line-height: 0; text-align: center; overflow-wrap: normal; word-spacing: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; margin: 0px; padding: 1px 0px; position: relative; font-family: IRANSans !important; font-size: 17px !important;"> X$ تعداد موفقیت در یک آزمایش دو جمله‌ای با ۱۰ نمونه و احتمال موفقیت $p = 0.5 " style="box-sizing: border-box; -webkit-tap-highlight-color: transparent; display: inline-block; line-height: 0; text-align: center; overflow-wrap: normal; word-spacing: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; margin: 0px; padding: 1px 0px; position: relative; font-family: IRANSans !important; font-size: 17px !important;">$ باشد. آنگاه نموداری که در تصویر زیر می‌بینید مقدار احتمال برای هر یک از تعداد موفقیت‌ها را نشان می‌دهد. مشخص است که این نمودار همان نمودار مربوط به تابع احتمال دو جمله‌ای است.

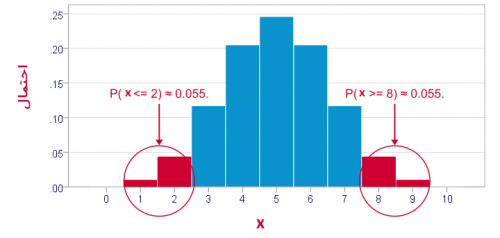
در نمودار بالا، مقدارهای بحرانی برای توزیع دو جمله‌ای را می‌بینید. بنابراین اگر $X " style="box-sizing: border-box; -webkit-tap-highlight-color: transparent; display: inline-block; line-height: 0; text-align: center; overflow-wrap: normal; word-spacing: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; margin: 0px; padding: 1px 0px; position: relative; font-family: IRANSans !important; font-size: 17px !important;"> X$ کمتر از ۲ یا بیشتر از ۸ باشد به نظر می‌رسد که احتمالات باید برابر با $0.055 " style="box-sizing: border-box; -webkit-tap-highlight-color: transparent; display: inline-block; line-height: 0; text-align: center; overflow-wrap: normal; word-spacing: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; margin: 0px; padding: 1px 0px; position: relative; font-family: IRANSans !important; font-size: 17px !important;"> ۰٫۰۵۵$ باشد.

بنابراین اگر این میزان احتمال را برای یک نمونه تصادفی بزرگتر از این مقدار مشاهده کنیم، به نظر می‌رسد که باید مشاهدات از چنین توزیعی نباشند.

در چنین حالتی قاعده تصمیم به صورت $X < x " style="box-sizing: border-box; -webkit-tap-highlight-color: transparent; display: inline-block; line-height: 0; text-align: center; overflow-wrap: normal; word-spacing: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; margin: 0px; padding: 1px 0px; position: relative; font-family: IRANSans !important; font-size: 17px !important;">$ برای آزمون یکطرفه چپ و $X > x " style="box-sizing: border-box; -webkit-tap-highlight-color: transparent; display: inline-block; line-height: 0; text-align: center; overflow-wrap: normal; word-spacing: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; margin: 0px; padding: 1px 0px; position: relative; font-family: IRANSans !important; font-size: 17px !important;"> X > x$ برای آزمون یکطرفه راست است.

بنابراین اگر مقدار احتمال هر یک از این حالت‌ها از مقدار خطای نوع اول کمتر باشد، فرض صفر در سطح آزمون $α " style="box-sizing: border-box; -webkit-tap-highlight-color: transparent; display: inline-block; line-height: 0; text-align: center; overflow-wrap: normal; word-spacing: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; margin: 0px; padding: 1px 0px; position: relative; font-family: IRANSans !important; font-size: 17px !important;"> α$ رد خواهد شد.

آزمون دو جمله‌ای در SPSS

در این نوشتار به منظور اجرای آزمون دو جمله‌ای، از نرم‌افزار SPSS استفاده کرده‌ایم. البته اگر می‌خواهید از نحوه اجرای این آزمون در زبان برنامه‌نویسی و محاسبات آماری R آگاه شوید بهتر است نوشتار آزمون علامت (Sign Test) — به زبان ساده را مطالعه کنید. به این ترتیب به نظر می‌رسد که می‌توان آزمون علامت را حالت خاصی از آزمون دو جمله‌ای در نظر گرفت.

نکته:

برای به کارگیری SPSS در حل مسائل مربوط به آزمون دو جمله‌ای بعنوان مثال:

فرض کنید فایل حاوی اطلاعاتی در مورد عنکبوت‌های ماده و نر موجود می باشد و قرار است به واسطه پانزده نمونه تصادفی، نسبت عنکبوت‌های نر را در جامعه آماری عنکبوت‌های خانگی آزمون کنیم. طبق یک نظریه، ادعا شده است که این نسبت برابر با $0.75 " style="box-sizing: border-box; -webkit-tap-highlight-color: transparent; display: inline-block; line-height: 0; text-align: center; overflow-wrap: normal; word-spacing: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; margin: 0px; padding: 1px 0px; position: relative; font-family: IRANSans !important; font-size: 17px !important;"> ۰٫۷۵$ است. از آنجایی که داده‌های مربوطه به صورت دو وضعیتی هستند، برای مشخص کردن نسبت یا احتمال موفقیت (مشاهده عنکبوت نر) از آزمون دو جمله‌ای استفاده خواهیم کرد. با سعی و تلاش فراوانی از گوشه گوشه‌های خانه تعداد ۱۵ عنکبوت جمع‌آوری و وضعیت جنسیت آن‌ها بررسی شده است. لازم به توضیح است که عنکبوت‌های ماده از نوع نر بزرگتر هستند.

به منظور شناخت از وضعیت و نسبت عنکبوت‌های درون نمونه بهتر است اطلاعاتی از وضعیت این داده‌ها ارائه کنیم.

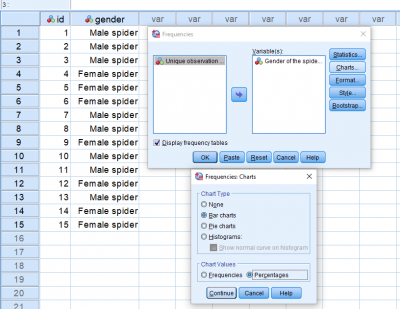جدول فراوانی و نمودار فراوانی می‌توانند به خوبی این کار را برایمان انجام دهند. کافی است از فهرست Analysis گزینه Descriptive Statistics و دستور Frequency را اجرا کنید.

همانطور که می‌بینید از نمودار Bar charts با مقدارهای درصدی Percentages استفاده شده است تا نمودار فراوانی به همراه برچسب مقدارها و فراوانی درصدی نمایش داده شود. البته برای اجرای این دستورات می‌توانید از کد زیر در پنجره Syntax نیز استفاده کنید.

خروجی این دستور به صورت زیر است. البته توجه داشته باشید برای نمایش تصویری فراوانی‌ها از نمودار میله‌ای استفاده کرده‌ایم به این ترتیب به نظر می‌رسد که درصد فراوانی برای عنکبوت‌های نر بیشتر از عنکبوت‌های ماده است. این ادعا توسط جدول فراوانی نیز تایید می‌شود. ولی نباید به همین جا اکتفا کنیم. شاید این اختلاف ناشی از نمونه بوده ولی در جامعه آماری چنین نباشد.

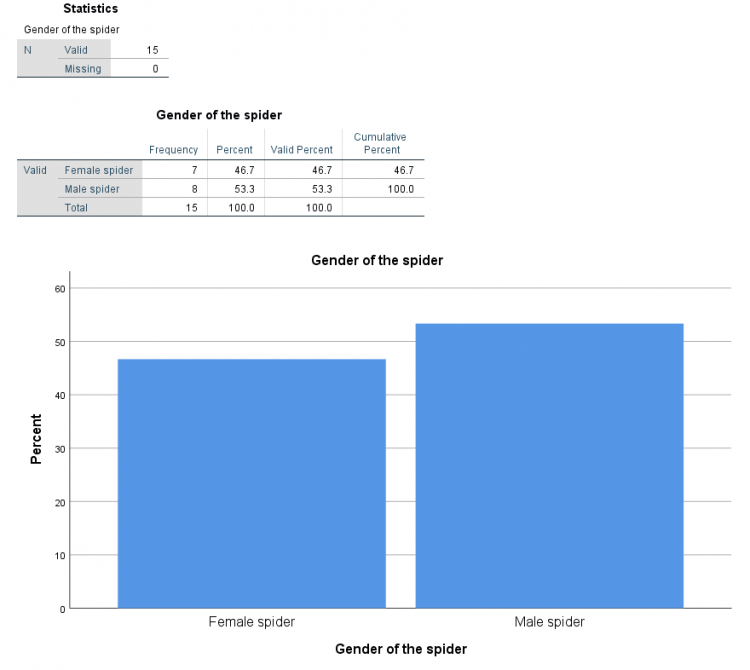بنابراین باید از یک آزمون آماری استفاده کنیم تا بتوانیم در مورد پارامتر جامعه قضاوت مناسب‌تری داشته باشیم. در اینجا با توجه به دو وضعیتی بودن مقدار متغیر، از آزمون دو جمله‌ای و توزیع دو جمله‌ای استفاده خواهیم کرد.

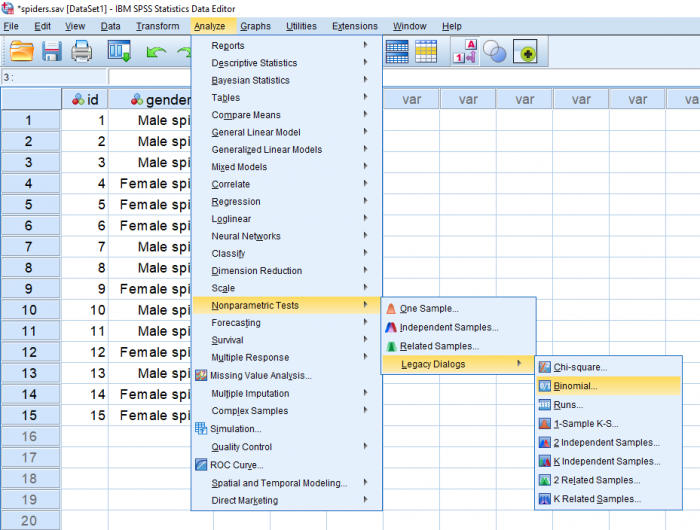
spider data file and binomial test

به منظور دسترسی به آزمون دوجمله‌ای در SPSS بهتر است مطابق تصویر بالا عمل کنید و از فهرست Analysis، گزینه Nonparametric Tests و انتخاب Legacy Dialogs و دستور Binomial را اجرا کنید. به این ترتیب پنجره مربوط به اجرای آزمون دوجمله‌ای مطابق باتصویر زیر ظاهر خواهد شد.

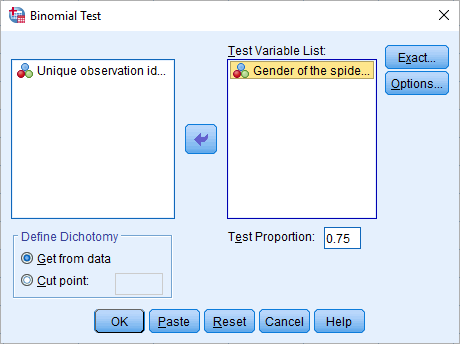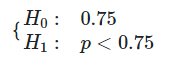همانطور که در تصویر بالا مشاهده می‌کنید، متغیر جنسیت عنکبوت‌ها در کادر Test Variable List قرار گرفته تا نشان دهد که آزمون باید برای این متغیر اجرا شود. در کادر test Proportion نیز مقداری که برای احتمال در فرض صفر در نظر گرفته شده، وارد می‌شود. با توجه به صورت مسئله این مقدار $0.75 " style="box-sizing: border-box; -webkit-tap-highlight-color: transparent; display: inline-block; line-height: 0; text-align: center; overflow-wrap: normal; word-spacing: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; margin: 0px; padding: 1px 0px; position: relative; font-family: IRANSans !important; font-size: 17px !important;"> ۰٫۷۵$ ثبت شده است. به این ترتیب فرضیات مربوط به این مسئله در زیر دیده می‌شود.

اگر لازم است می‌توانید با استفاده از کادر Define Dichotomy مشخص کنید که متغیر معرفی شده دو مقداری است یا باید توسط یک نقطه برش به دو گروه تفکیک شود. برای این کار کافی است با انتخاب Cut point مقداری که محل برش را تعیین می‌کند، مشخص کنید.

نکته: اگر از پنجره Syntax و کد نویسی در SPSS استفاده می‌کنید، کافی است دستورات زیر را به کار برید.

با فشردن دکمه OK خروجی این آزمون به صورت زیر خواهد بود. مشخص است که با توجه به مقدار Sig و مقایسه آن با $α = 0.05 " style="box-sizing: border-box; -webkit-tap-highlight-color: transparent; display: inline-block; line-height: 0; text-align: center; overflow-wrap: normal; word-spacing: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; margin: 0px; padding: 1px 0px; position: relative; font-family: IRANSans !important; font-size: 17px !important;"> α = ۰٫۰۵$ فرض صفر را رد نخواهیم کرد زیرا به نظر می‌رسد که مقدار احتمال (Exact Sig) از احتمال خطای نوع اول ( $α " style="box-sizing: border-box; -webkit-tap-highlight-color: transparent; display: inline-block; line-height: 0; text-align: center; overflow-wrap: normal; word-spacing: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; margin: 0px; padding: 1px 0px; position: relative; font-family: IRANSans !important; font-size: 17px !important;"> α$ ) بیشتر است. پس نمونه دلیلی برای رد فرض صفر ارائه نکرده است.

نکته: باید توجه داشت که آزمون دو جمله‌ای، اولین مقدار در ستون متغیر را به عنوان موفقیت در نظر می‌گیرد. بنابراین از آنجایی که برای اولین مشاهده مقدار جنسیت برابر با ۱ یعنی عنکبوت نر ثبت شده، آزمون در مورد نسبت عنکبوت‌های نر خواهد بود.

در جدول Binomial Test مشخص است که در ستون Observed Prop برای مشاهده عنکبوت ماده حدود $0.47 " style="box-sizing: border-box; -webkit-tap-highlight-color: transparent; display: inline-block; line-height: 0; text-align: center; overflow-wrap: normal; word-spacing: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; margin: 0px; padding: 1px 0px; position: relative; font-family: IRANSans !important; font-size: 17px !important;"> ۰٫۴۷$ و برای عنکبوت نر برابر با $0.53 " style="box-sizing: border-box; -webkit-tap-highlight-color: transparent; display: inline-block; line-height: 0; text-align: center; overflow-wrap: normal; word-spacing: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; margin: 0px; padding: 1px 0px; position: relative; font-family: IRANSans !important; font-size: 17px !important;">$ است. فاصله مقدار $0.53 " style="box-sizing: border-box; -webkit-tap-highlight-color: transparent; display: inline-block; line-height: 0; text-align: center; overflow-wrap: normal; word-spacing: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; margin: 0px; padding: 1px 0px; position: relative; font-family: IRANSans !important; font-size: 17px !important;"> ۰٫۵۳$ تا $0.75 " style="box-sizing: border-box; -webkit-tap-highlight-color: transparent; display: inline-block; line-height: 0; text-align: center; overflow-wrap: normal; word-spacing: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; margin: 0px; padding: 1px 0px; position: relative; font-family: IRANSans !important; font-size: 17px !important;">$ باعث نشده است تا فرض صفر رد شود. در نتیجه اختلاف بین درصدها بین فرض صفر و نتیجه حاصل از نمونه، ناشی از خطای نمونه‌گیری است و این اختلاف در جامعه آماری وجود ندارد. به این معنی که درصد عنکبوت‌های نر در جامعه آماری همان نسبت $0.75 " style="box-sizing: border-box; -webkit-tap-highlight-color: transparent; display: inline-block; line-height: 0; text-align: center; overflow-wrap: normal; word-spacing: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; margin: 0px; padding: 1px 0px; position: relative; font-family: IRANSans !important; font-size: 17px !important;"> ۰٫۷۵$ است. باز هم توجه داشته باشید که در پانوشته جدول Binomial Test مشخص شده که فرض مقابل به صورت $< 0.75 " style="box-sizing: border-box; -webkit-tap-highlight-color: transparent; display: inline-block; line-height: 0; text-align: center; overflow-wrap: normal; word-spacing: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; margin: 0px; padding: 1px 0px; position: relative; font-family: IRANSans !important; font-size: 17px !important;"> < 0.75$ است در نتیجه آزمون یک طرفه خواهد بود.

حال در نظر بگیرید که قرار است آزمون را برای نسبت عنکبوت‌های ماده اجرا کنیم. کافی است هفت مشاهده اول را برای عنکبوت‌های ماده و هشت مشاهده بعدی را برای عنکبوت‌های نر در نظر بگیریم. به این ترتیب می‌توانیم با استفاده از وزن‌‌دهی به مشاهدات این اطلاعات را به طور خلاصه در SPSS‌ وارد کنیم. به تصویر زیر دقت کنید.

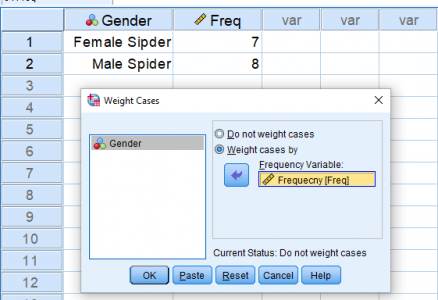با این کار فراوانی‌ها را در ستون Freq و مقدار را در ستون Gender‌ وارد کرده‌ایم. به این ترتیب مقدار ۰ که برای عنکبوت‌های ماده تعریف شده، هفت بار و مقدار ۱ که برای عنکبوت‌های نر در نظر گرفته شده، ۸ بار در آزمون دو جمله‌ای محسوب می‌شوند.

حال به اجرای آزمون دو جمله‌ای بر این اساس می‌پردازیم. مشخص است که با توجه به اینکه اولین مقدار مربوط به عنکبوت‌های ماده است، نسبت این گونه از عنکبوت‌ها در آزمون دو جمله‌ای مورد بررسی قرار می‌گیرد. نتیجه اجرا در این صورت مطابق با تصویر زیر است.

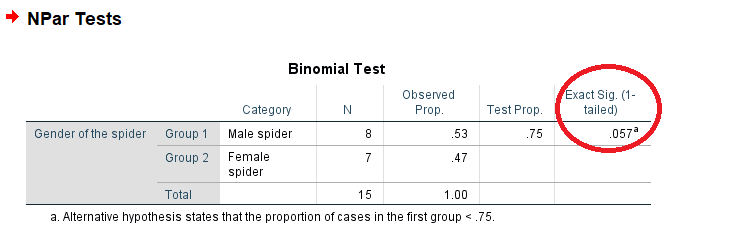با توجه به آزمون یکطرفه و مقدار Exact Sig که در ستون آخر جدول Binomial Test نوشته شده، در سطح خطای $0.05 " style="box-sizing: border-box; -webkit-tap-highlight-color: transparent; display: inline-block; line-height: 0; text-align: center; overflow-wrap: normal; word-spacing: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; margin: 0px; padding: 1px 0px; position: relative; font-family: IRANSans !important; font-size: 17px !important;"> ۰٫۰۵$ فرض صفر رد می‌شود.

در نتیجه نمی‌توان درصد عنکبوت‌های ماده را برابر با $0.75 " style="box-sizing: border-box; -webkit-tap-highlight-color: transparent; display: inline-block; line-height: 0; text-align: center; overflow-wrap: normal; word-spacing: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; margin: 0px; padding: 1px 0px; position: relative; font-family: IRANSans !important; font-size: 17px !important;"> ۰٫۷۵$ در نظر گرفت.

آنچه که گفته شد، مسیر دسترسی به دستور مستقیم آزمون دو جمله‌ای و شکل و شیوه تفسیر خروجی‌های آن بود.

شیوه جدید دسترسی مستقیم آزمون دو جمله ای:

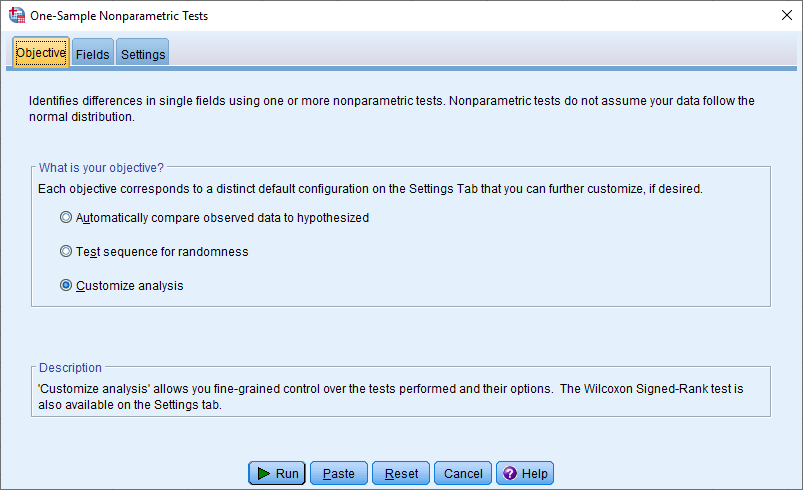
می‌توانید گزینه One Sample را از گزینه Nonparametric Tests انتخاب کرده و تنظیمات را به شکلی در‌آورید که آزمون دو جمله‌ای اجرا شود. ابتدا لازم است که نوع آزمون را مشخص کنید. در تصویر زیر درخواست شده که آزمون توسط کاربر انتخاب شود زیرا گزینه Customize Analysis‌ فعال شده است.

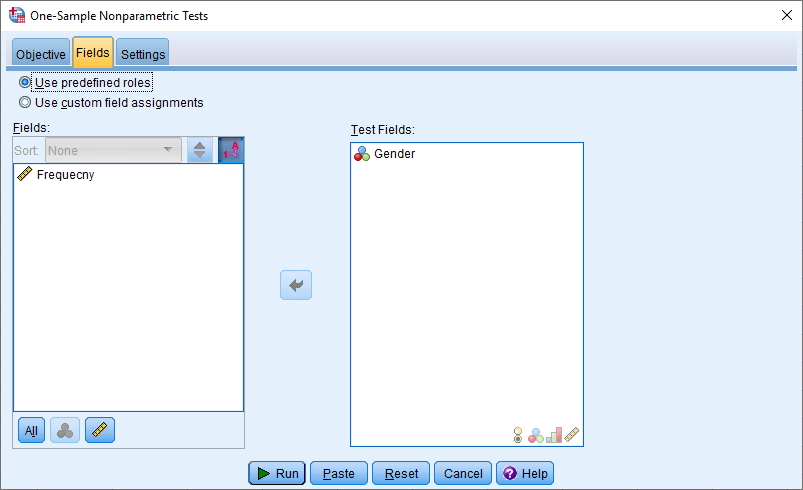
با انتخاب برگه Fields، متغیرهایی که باید در آزمون به کار گرفته شوند، تعیین می‌شود. البته ممکن است SPSS با توجه به نقشی که هر یک از متغیرها دارند، بطور خودکار این کار را انجام دهد. واضح است که متغیر Gender باید به عنوان متغیر مورد نظر انتخاب شود.

در بخش انتهایی نیز باید نوع آزمون و شیوه اجرای آن تنظیم شود. برگه Settings این وظیفه را به عهده دارد. بنابراین با انتخاب گزینه Customize tests و (Compare observed binary probability to hypothesized (binomial test نوع آزمون را دو جمله‌ای مشخص خواهید کرد.

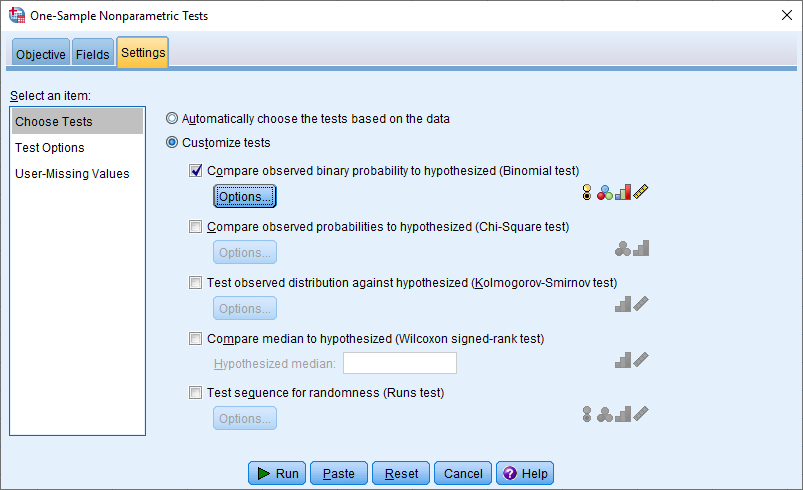
اگر لازم است تنظیماتی نظیر تعیین مقدار احتمال در فرض صفر یا انتخاب مقدار متغیر به عنوان مقدار موفقیت صورت بگیرید از دکمه Options مربوط به این آزمون استفاده کنید. برای پاسخ به مسئله مربوط به عنکبوت‌های ماده کافی است تنظیمات را مطابق با تصویر زیر تعیین کنید.

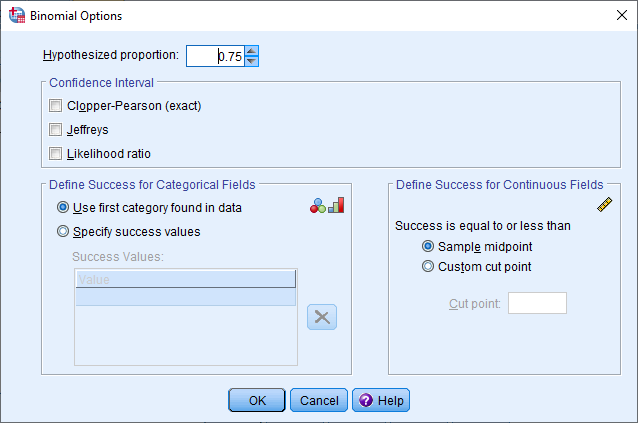با فشردن دکمه Run در پنجره اصلی، آزمون اجرا شده و نتایج مطابق با تصویر زیر ظاهر خواهند شد. البته توجه دارید که باید نتیجه‌ها مطابق با مثال قبل باشند.

خروجی‌هایی که توسط دستورات جدید در SPSS ایجاد می‌شوند، شامل اطلاعاتی بیشتری نیز هستند. همانطور که می‌بینید در ستون Decision مشخص است که فرض صفر در سطح خطای $0.05 " style="box-sizing: border-box; -webkit-tap-highlight-color: transparent; display: inline-block; line-height: 0; text-align: center; overflow-wrap: normal; word-spacing: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; margin: 0px; padding: 1px 0px; position: relative; font-family: IRANSans !important; font-size: 17px !important;"> ۰٫۰۵$ رد می‌شود.

البته با توجه به ستون Sig این امر مطابق با خروجی‌های قبلی همین نتیجه را خواهد داد. اگر روی این جدول دوبار کلیک کنید، وارد صفحه‌ای می‌شوید که اطلاعات بیشتری در مورد آزمون و متغیرها در خود دارد. چنین پنجره‌هایی به Model Viewer معروف هستند. در تصویر زیر پنجره‌ Model Viewer برای آزمون دو جمله‌ای را می‌بینید

. سمت راست نمودارها و آماره‌های توصیفی و سمت چپ نیز نتیجه اجرای آزمون دو جمله‌ای دیده می‌شود.

09357258425

www.pajuha.ir

info@pajuha.ir

سفارش ترجمه تخصصی

تحلیل آماری AHP ANP SPSS PLS

سمیه پنج‌شنبه 5 دی 1398 ساعت 11:57

گروه پژوهشی آینده

گروه پژوهشی آینده