مجموعه پرسشنامه های مدیریت (بخش دوم)

مجموعه پرسشنامه های مدیریت (بخش دوم)

pm292.پرسشنامه ویژگی های کارکنان در مدیریت عملکرد Reymond A. Noe (2000).docx

pm294.پرسشنامه مهارت های مدیریتDavid Whetten و همکاران (۲۰۰۰).docx

pm295.پرسشنامه مدیر اثربخش Tricia Vilkinas و همکاران (۲۰۰۱).docx

pm296.پرسشنامه ویژگی های روان سنجی مهارت های مدیریتی Frank Shipper (1999).docx

pm297.پرسشنامه مهارت های سازمانی Farhad Analoui (1995).docx

pm298.پرسشنامه شایستگی های مدیریت ارشد Chris Pierce (1995).docx

pm299.پرسشنامه شایستگی های مدیران در زمینه فناوری اطلاعات و ارتباطات Schiller (2003).docx

pm300.پرسشنامه اثربخشی مدیریت ارشد Analoui (1995).docx

pm301.پرسشنامه فعالیت های مدیریتی فایول مقیمی (۱۳۵۰).docx

pm302.پرسشنامه مهارت های ادراکی، انسانی و فنی Kaufman (1999).docx

pm303.پرسشنامه یادگیری در مورد محیط مدیران Graham (2006).docx

pm304.پرسشنامه ظرفیت یادگیری سازمانی Chiva و همکاران (۲۰۰۷).docx

pm305.پرسشنامه سازمان یادگیرنده Gardiner (1999).docx

pm306.پرسشنامه سازمان یادگیرنده بر اساس مدل DLOQ Dima Jamali و همکاران (۲۰۰۹).docx

pm307.پرسشنامه سبک تصمیم گیری شخصی Arash Shahin و همکاران (۲۰۰۷).docx

pm308.پرسشنامه تصمیم گیرنده خوب بودن Russell A. Matthews و همکاران (۲۰۰۳).docx

pm309.پرسشنامه برنامه ریز خوب بودن Russell A. Matthews و همکاران (۲۰۰۳).docx

pm310.پرسشنامه مشارکت در تصمیم گیری گروهی Andrei Mikhailitchenko و همکاران (۲۰۰۶).docx

pm311.پرسشنامه سبک پاسخگویی Annette L. M و همکاران (۲۰۰۶).docx

pm312.پرسشنامه سبک تصمیم گیری کلی David P. Spicer و همکاران (۲۰۰۵).docx

pm313.پرسشنامه دودلی و تردید در تصمیم گیری Muel Kaptein و همکاران (۲۰۰۵).docx

pm314.پرسشنامه استراتژی تصمیم گیری Read Elaydi (2006).docx

pm315.پرسشنامه ساختار نامشهود سازمان Rodney Overton (2007).docx

pm316.پرسشنامه نگرش نسبت به افراد و سازمان M. Scott Myers (1970).docx

pm317.پرسشنامه مدیریت فرایند سازماندهی و سازمان غیر رسمی Muel Kaptein و همکاران (۲۰۰۵).docx

pm318.پرسشنامه سازماندهی و توسعه ساختار سازمانی Muel Kaptein و همکاران (۲۰۰۵).docx

pm320.پرسشنامه ساختار سازمانی Frank (2006).docx

pm321.پرسشنامه ابعاد ساختار سازمانی John Andy Wood (2005).docx

pm322.پرسشنامه ساختار سازمانی بروکراتیک Sandra S. Liu (2002).docx

pm323.پرسشنامه خود نظارتی John W و همکاران (۲۰۰۲).docx

pm324.پرسشنامه فرآیند کنترل Wayhe H. Bovey (2001)

pm325.پرسشنامه بازخورد عملکرد Wayne H. Bovey و همکاران (۲۰۰۱).pdf

pm326.پرسشنامه انواع بازخورد Galbraith et al (2002)

pm327.پرسشنامه مهارت های نظارت John W. Newstorm و همکاران (۲۰۰۲).docx

pm328.پرسشنامه کنترل پیش نگر Graeme Martin (2006).docx

pm329.پرسشنامه آمادگی برای تغییر Graham S. Lowe (2006).docx

pm330.پرسشنامه مکانیزم های دفاعی در برابر تغییر Wayhe H. Bovey و همکاران (۲۰۰۱).docx

pm331.پرسشنامه تغییر سازمانی Mel silberman (2003).docx

pm332.پرسشنامه مقاومت نسبت به تغییر سازمانی Wayne H. Bovey و همکاران (۲۰۰۱).docx

pm333.پرسشنامه پاسخ سازمان به تغییر Galbraith et al (2002).docx

pm334.پرسشنامه تغییر محیط کاری با کیفیت بالا Graham S. Lowe (2006).docx

pm335.پرسشنامه انعطاف پذیری نسبت به تغییر Penny Gardiner (1999).docx

pm336.پرسشنامه تغییر سازمانی Mel silberman (2003).docx

pm337.پرسشنامه آمادگی تغییر Ricardo Chiva و همکاران (۲۰۰۷).docx

pm338.پرسشنامه آمادگی سازمانی برای تغییر با رویکرد منابع انسانی Ralph Chritensen (2006).docx

pm339.پرسشنامه تجربه تغییر Rodney Overton (2007).docx

pm340.پرسشنامه مداخلات Kurmet Kivipold و همکاران (۲۰۱۰).docx

pm341.پرسشنامه بهبود سازمانی Rodney Overton (2007).docx

pm342.پرسشنامه توسعه سازمانی Peter Lok و همکاران (۲۰۰۰).docx

pm343.پرسشنامه علائم تحلیل رفتگی دکتر سید محمد مقیمی و دکتر مجید رمضان(۱۳۹۴).docx

ادبیات مبانی نظری

مقدمه

یکی از بخش‏های مهم تحقیق، بخش مربوط به پیشینه و ادبیات تحقیق است؛ یعنی یکی از کارهای ضروری در هر پژوهشی، مطالعه منابع2 مربوط به موضوع تحقیق است؛ زیرا سرچشمه علوم را می‌توان در پیشینه آنها کاوش کرد (دمپی یر، 2006، ص 1).

جان دیوئی اعتقاد دارد مطالعه منابع، به محقق کمک می‏کند تا بینش عمیقی نسبت به جنبه‏های مختلف موضوع تحقیق پیدا کند. مطالعه منابع، باید هم از منابعی باشد که به طور مستقیم، در رابطه با موضوع تحقیق می‏باشند و هم از منابعی باشند که به صورت غیرمستقیم با آن موضوع، ارتباط دارند(دلاور، 1375، ص 182).

در این بخش این مسائل مطرح است:

الف) پیشینه تحقیق چیست؟

ب) اهمیت پیشینه تحقیق چیست؟

ج) اهداف پیشینه‌یابی تحقیق کدامند؟

د) منابع مهم پیشینه تحقیق کدامند؟

ه) روش‏های پیشینه تحقیق چه می‏باشند؟

از این رو، به نظر برخی از فلاسفه آموزشی، مانند جان لاک، هدف آموزش کارآمد، این است که شخص ضمن آشنایی با دانش لازم، طوری بار آورده شود که روش‌های کاویدن جهان موضوعات را به خوبی انجام دهد(فراست، 2006، ص 308).

اهمیت پیشینه کاوی در تحقیق

یک پژوهش‌گر، قبل از انجام تحقیق و بعد از انتخاب موضوع و تدوین عنوان و قبل از نگارش طرح تحقیق، نیاز دارد که با مراجعه به مدارک و اسناد، پیرامون موضوع و مسئله‏ای که برای تحقیق انتخاب کرده است، آگاهی خود را گسترش دهد؛ تا بتواند در پرتو اطلاعات به دست آمده، مسئله تحقیق و متغیر‏های خود را دوباره تعریف و معین کند و کرانه‏های آنها را مشخص سازد. این امر به او کمک می‏کند تا تحقیقات خود را در راستای مجموعه پژوهش‏های هم خانواده قرار دهد و آن را با دستاوردهای تحقیقاتی دیگران هماهنگ کند.

بررسی تأثیر ساختار سرمایه برارزش شرکت ، نرخ بازده سرمایه و سود هر سهم شرکت های پذیرفته شده در بورس اوراق بهادار تهران

بررسی رفتارسپرده ها درصنعت بانکداری ایران با استفاده از آزمون همگرایی

تشریح کامل مفاهیم سرمایه انسانی و عملکرد کارکنان

بررسی تاثیر اعتبار تجاری، اهرم مالی و بازده مورد انتظار سهام بر ریسک اطلاعات شرکت‌ها

بررسی رابطه بین عدالت در پرداخت با رضایتمندی شغلی (مطالعه موردی: بخش بیمه و درمان سازمان تامین اجتماعی استان ایلام)

تعیین رابطه مولفه‌ها و عناصر بسته‌بندی با خرید محصولات مواد غذایی توسط مصرف‌کنندگان استان ایلام

ارزیابی عملکرد دانشگاه علوم پزشکی یاسوج براساس مدل تعالی سازمانیEFQM

ارائه الگوی اعتماد سازمانی با رویکرد اسلامی

شناسایی و الویت بندی عوامل موثر بر موفقیت در هتل های4 و 5 ستاره تهران از دیدگاه مدیران ارشد و مدیران میانی

تأثیر ابعاد کیفیّت خدمات بانکی برتجهیز منابع بانکها

تاثیربکارگیری شیوه های مدیریت زنجیره تأمین دربهبود عملکرد سازمانی از طریق مزیّت رقابتی

بررسی تاثیر جو اخلاق سازمانی برمدیریت دانش در سازمان اموراقتصادی و دارایی و اداره کل امورمالیاتی استان گیلان

بررسی تاثیر رهبری خدمتگزار بر اعتماد سازمانی و توانمند سازی کارکنان با توجه به سابقه خدمت و سطح تحصیلات در صدا و سیمای مرکز گیلان

تاثیرارتباطات بین فردی بر رضایت و وفاداری مشتریان در صنعت بانکداری (مورد: شعب بانک صادرات استان قزوین)

ارزیابی کارایی رتبه بندی شرکت های پذیرفته شده در بورس اوراق بهادار ایران

بررسی اثر تعطیلات در بازار بورس اوراق بهادار تهران

انتخاب مرغ سبز و محصولات ارگانیک

بررسی رابطه بین تبلیغات موبایلی و قصد خرید مصرف کنندگان (مطالعه موردی: فروشگاههای پوشاک مردانه شهرستان رشت)

نقش مدیریت ریسک مالی بر ارزش شرکت ها

رابطه بین فرسودگی شغلی وابعاد آن بر تعهد سازمانی دبیران ناحیه 1رشت

تاثیر اعتماد و خودآگاهی کارکنان بر تمایل به اشتراک دانش با توجه به نقش میانجیگری امنیت روانشناختی در دانشگاه علوم پزشکی گیلان

تبیین رابطه بین کیفیت سود در شرکتهای ورشکسته در مقایسه با شرکتهای غیر ورشکسته

بررسی اثر ساختار نظام راهبری بر ارتباط بین جریان وجوه نقد آزاد مازادومدیریت سود

بررسی رابطه ی بین عوامل سازمانی و هوش بازاریابی در بانک ملی ایران (مطالعه موردی بانک ملی شهرستان زنجان)

بررسی تأثیر سیستم برنامه ریزی منابع سازمانی بر عملکرد زنجیره تأمین در شرکت ایران خودرو

ارزیابی عوامل موثر بر قصد استفاده از آموزش الکترونیکی در آموزش ضمن خدمت وزارت نیرو

بررسی رابطه CRM با کیفیت خدمات ارائه شده در بانک ( مطالعه موردی : کلیه شعب بانک ملت استان گیلان)

بررسی ارتباط بین ساختار سرمایه با سودآوری بانک های پذیرفته شده در بورس اوراق بهادار تهران

ارزیابی فاکتورهای تاثیرگذار بر استفاده بهینه از فن آوری اطلاعات در صنعت بیمه سلامت در استان گیلان

#ترجمه_آماده
#دانلود_مقاله
#دانلودمبانی-نظری-پایاننامه
#دانلودپرسشنامه-مدیریت
#دانلودپرسشنامهروان_شناسی

شماره تماس جهت سفارش: 09353761841

ادرس سایت:Www.pajuha.com

آموزش آزمون دو جمله ای در spss

آزمون دو جمله‌ ای

فرض کنید یک جامعه آماری با داده‌های دو وضعیتی در اختیار دارید . به کمک آزمون دو جمله‌ای می‌توانیم به سوالاتی نظیر فهرست زیر در مورد این جامعه پاسخ دهیم.

• آیا می‌توان گفت که ۵۰٪ افراد جامعه، مرد هستند؟
• آیا، نسبت استفاده از وسایل حمل نقل عمومی در جامعه برابر با ۴۰٪ است؟
• آیا می‌توان گفت که نسبت مصرف کنندگان اینترنت همراه به تعداد کل سیمکارت کمتر از ۳۰٪ است.
• …

به تصویر زیر توجه کنید. به نظر می‌رسد که نمونه‌هایی از جامعه با متغیرهایی دو وضعیتی تهیه شده و قرار است براساس نمونه برای پارامتر نسبت گوی‌های قرمز و آبی دست به قضاوت بزنیم.

در این تصویر با سه جامعه مواجه هستیم. جامعه سمت راست، شامل پارامتر نسبت گوی‌های $$p=0.75$$ است و نمونه از همه آن‌ها تهیه شده است.

در جامعه دوم نسبت گوی‌های قرمز به آبی برابر با ۵۰٪ است و البته این قاعده در نمونه نیز دیده می‌شود.

در تصویر سمت چپ، نسبت گوی‌های قرمز به آبی ۲۵٪ است که البته در نمونه چنین چیزی دیده نمی‌شود در نتیجه ممکن است رای یا قضاوت ما در مورد این جامعه توسط نمونه آبی بودن همه اعضا باشد.

همانطور که دیده می‌شود ممکن است نمونه‌های مختلفی از هر جامعه تهیه شود. بنابراین سه شکل یا حالت مختلف (که با خطوط نارنجی مشخص شده‌اند) برای نمونه گرفته شده از جامعه سمت راست دیده می‌شود که هر کدام ممکن است برآورد متفاوتی از جامعه واقعی ارائه دهند. به این ترتیب وجود یک آزمون آماری که بتواند با دقت مناسب براساس یک نمونه در مورد پارامتر جامعه دید مناسبی به ما بدهد، ضروری است.

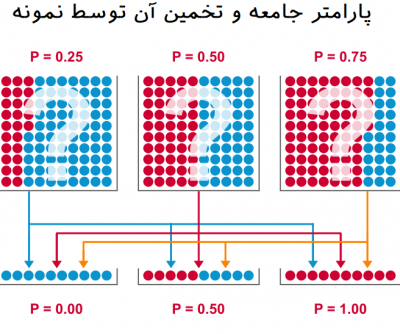متاسفانه ممکن است نمونه‌ها گواه یا معیاری خوبی برای تشخیص اطلاعات و پارامترهای واقعی جامعه نباشند. جالب است که این تصویر نشان می‌دهد، گاهی ممکن است براساس نمونه و انجام آزمون دچار خطا شده و به نادرستی نسبت را پیش‌بینی کنیم. البته می‌دانیم که این اشکال به خطای نمونه‌گیری یا به نوعی توان آزمون بستگی دارد.

اساس و پایه آزمون فرض آماری بر نمونه و توزیع آماره آزمون قرار گرفته است. به این ترتیب سعی داریم به کمک نمونه تصادفی در مورد خصوصیات جامعه آماری قضاوت کنیم. در آزمون فرض آماری، ابتدا حدس یا نظری در مورد پارامتر جامعه داریم، سپس با نمونه‌گیری و محاسبات مرتبط با آن، سعی داریم که این حدس یا فرضیه اولیه را مورد آزمایش یا آزمون قرار دهیم. این فرضیه را «فرض صفر» (Null Hypothesis) می‌نامیم.

ممکن است بعضی از مقدارهای حاصل از نمونه بسیار از فرض اولیه دور باشند در نتیجه نمی‌توانیم آن‌ها را تاییدی بر این فرض در نظر بگیریم در نتیجه آن فرض را رد می‌کنیم. ولی اگر نمونه بتواند فرضیه اولیه را مورد تایید قرار دهد، خواهیم گفت نمونه دلیلی برای رد فرض صفر ندارد ولی توجه داشته باشید که هرگز نمی‌توان گفت که فرض صفر صحیح است زیرا ممکن است یک نمونه دیگر، دلیلی بر رد فرض صفر ارائه کند.

با توجه به اینکه در آزمون دو جمله‌ای با متغیرهای دو وضعیتی مواجه هستیم، سوال اصلی در اینجا می‌تواند به این صورت نوشته شود: «آیا احتمال آنکه از بین ۱۰ نمونه تصادفی ۲ موفقیت حاصل شود، برابر با ۰٫۵ است؟»

برای پاسخ به این پرسش از آزمون دو جمله‌ای استفاده خواهیم کرد. ابتدا فرضیات و شرایط مربوط به این آزمون را مورد بررسی قرار می‌دهیم.

شرایط آزمون دو جمله‌ای

از آنجایی که این آزمون از نوع ناپارامتری است، وجود توزیع نرمال برای داده‌ها الزامی نیست. البته باید توجه داشت که در اینجا با داده‌های دو وضعیتی مواجه هستیم. بنابراین توزیع چنین داده‌هایی دو جمله‌ای خواهد بود.

البته ممکن است داده‌های حاصل از نمونه به صورت کمی باشند ولی با استفاده از یک نقطه برش می‌توانیم آن‌ها را به دو طبقه یا دو وضعیت تفکیک کنیم.

مثال:

• اگر بخواهیم آزمونی  که درصد افرادی که بازنشسته هستند (بالای ۶۰ سال سن دارند) آیا با ۳۰٪ برابر است با خیر. بگیریم .
• به این ترتیب یک متغیر کمی را بوسیله برش از مقدار ۶۰ به دو گروه بالای ۶۰ سال و زیر ۶۰ سال شکسته‌ایم.
• البته توجه داشته باشید که اگر مقدار احتمال در فرض صفر به صورت $$p=0.5$$ باشد، می‌توانیم از آزمون علامت نیز برای حل این مسئله استفاده کنیم.
• در این حالت به نظر می‌رسد که نقطه برش می‌تواند همان میانه در نظر گرفته شود زیرا ۵۰٪ داده‌ها از آن بزرگتر یا کوچکتر هستند.

مثال۲:

فرض کنید یک نمونه تصادفی از افراد جامعه تهیه کرده‌ایم. از هر یک از این افراد سنشان را پرسیده و ثبت کرده‌ایم. بنا به مقادیر حاصل از سن افراد متغیر جدیدی تعریف می‌کنیم که مقدار آن برای افرادی که بیش از ۶۰ سال سن دارند برابر با ۱ و در غیراینصورت برابر با ۰ است. به این ترتیب از روی متغیر کمی سن یک متغیر کیفی با دو وضعیت ایجاد کرده‌ایم که می‌تواند در آزمون علامت یا در آزمون دو جمله‌ای به کار رود.

اگر  متغیر تصادفی با توزیع دو جمله‌ای باشد، آنگاه شکل تابع احتمال آن به صورت زیر خواهد بود.

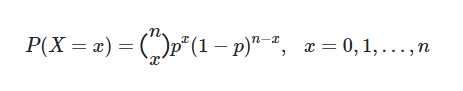
در این صورت می‌نویسیم ‌ است. هر یک از این پارامترها را در ادامه معرفی کرده‌ایم.

• تعداد نمونه در اینجا برابر با است.
• تعداد موفقیت‌ها در اینجا برابر با  است.
• احتمال موفقیت در هر بار آزمایش برنولی برای اعضای جامعه آماری ثابت و برابر با  است.

واضح است که منظور از تعداد ترکیبات  از  است. فرض کنید که  تعداد موفقیت در یک آزمایش دو جمله‌ای با ۱۰ نمونه و احتمال موفقیت  باشد. آنگاه نموداری که در تصویر زیر می‌بینید مقدار احتمال برای هر یک از تعداد موفقیت‌ها را نشان می‌دهد. مشخص است که این نمودار همان نمودار مربوط به تابع احتمال دو جمله‌ای است.

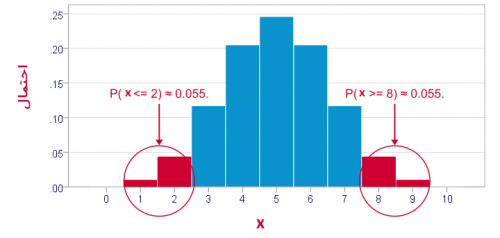
در نمودار بالا، مقدارهای بحرانی برای توزیع دو جمله‌ای را می‌بینید. بنابراین اگر  کمتر از ۲ یا بیشتر از ۸ باشد به نظر می‌رسد که احتمالات باید برابر با  باشد.

بنابراین اگر این میزان احتمال را برای یک نمونه تصادفی بزرگتر از این مقدار مشاهده کنیم، به نظر می‌رسد که باید مشاهدات از چنین توزیعی نباشند.

در چنین حالتی قاعده تصمیم به صورت  برای آزمون یکطرفه چپ و $$X>x$$ برای آزمون یکطرفه راست است.

بنابراین اگر مقدار احتمال هر یک از این حالت‌ها از مقدار خطای نوع اول کمتر باشد، فرض صفر در سطح آزمون  رد خواهد شد.

آزمون دو جمله‌ای در SPSS

در این نوشتار به منظور اجرای آزمون دو جمله‌ای، از نرم‌افزار SPSS استفاده کرده‌ایم. البته اگر می‌خواهید از نحوه اجرای این آزمون در زبان برنامه‌نویسی و محاسبات آماری R آگاه شوید بهتر است نوشتار آزمون علامت (Sign Test) — به زبان ساده را مطالعه کنید. به این ترتیب به نظر می‌رسد که می‌توان آزمون علامت را حالت خاصی از آزمون دو جمله‌ای در نظر گرفت.

نکته:

برای به کارگیری SPSS در حل مسائل مربوط به آزمون دو جمله‌ای بعنوان مثال:

فرض کنید  فایل حاوی اطلاعاتی در مورد عنکبوت‌های ماده و نر موجود می باشد و قرار است به واسطه پانزده نمونه تصادفی، نسبت عنکبوت‌های نر را در جامعه آماری عنکبوت‌های خانگی آزمون کنیم. طبق یک نظریه، ادعا شده است که این نسبت برابر با  است. از آنجایی که داده‌های مربوطه به صورت دو وضعیتی هستند، برای مشخص کردن نسبت یا احتمال موفقیت (مشاهده عنکبوت نر) از آزمون دو جمله‌ای استفاده خواهیم کرد. با سعی و تلاش فراوانی از گوشه گوشه‌های خانه تعداد ۱۵ عنکبوت جمع‌آوری و وضعیت جنسیت آن‌ها بررسی شده است. لازم به توضیح است که عنکبوت‌های ماده از نوع نر بزرگتر هستند.

به منظور شناخت از وضعیت و نسبت عنکبوت‌های درون نمونه بهتر است اطلاعاتی از وضعیت این داده‌ها ارائه کنیم.

جدول فراوانی و نمودار فراوانی می‌توانند به خوبی این کار را برایمان انجام دهند. کافی است از فهرست Analysis گزینه Descriptive Statistics و دستور Frequency را اجرا کنید.

همانطور که می‌بینید از نمودار Bar charts با مقدارهای درصدی Percentages استفاده شده است تا نمودار فراوانی به همراه برچسب مقدارها و فراوانی درصدی نمایش داده شود. البته برای اجرای این دستورات می‌توانید از کد زیر در پنجره Syntax نیز استفاده کنید.

 

خروجی این دستور به صورت زیر است. البته توجه داشته باشید برای نمایش تصویری فراوانی‌ها از نمودار میله‌ای استفاده کرده‌ایم به این ترتیب به نظر می‌رسد که درصد فراوانی برای عنکبوت‌های نر بیشتر از عنکبوت‌های ماده است. این ادعا توسط جدول فراوانی نیز تایید می‌شود. ولی نباید به همین جا اکتفا کنیم. شاید این اختلاف ناشی از نمونه بوده ولی در جامعه آماری چنین نباشد.

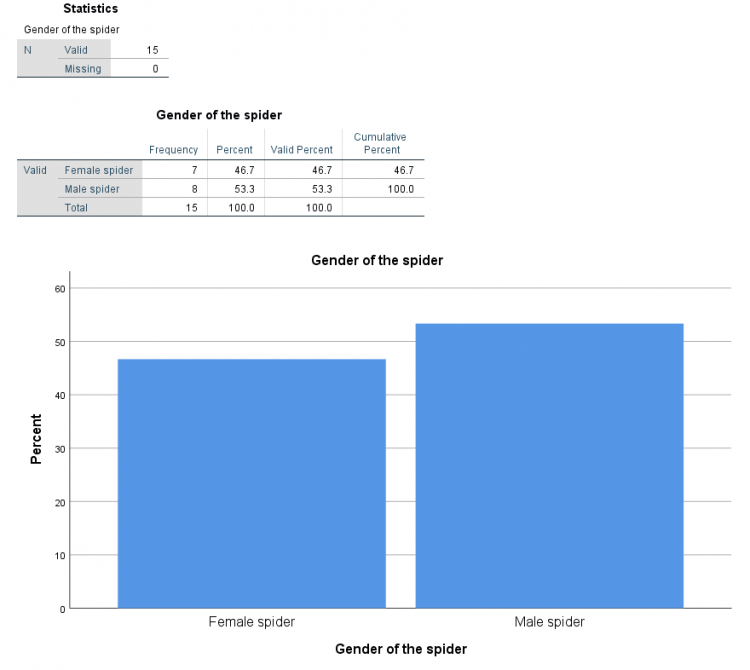بنابراین باید از یک آزمون آماری استفاده کنیم تا بتوانیم در مورد پارامتر جامعه قضاوت مناسب‌تری داشته باشیم. در اینجا با توجه به دو وضعیتی بودن مقدار متغیر، از آزمون دو جمله‌ای و توزیع دو جمله‌ای استفاده خواهیم کرد.

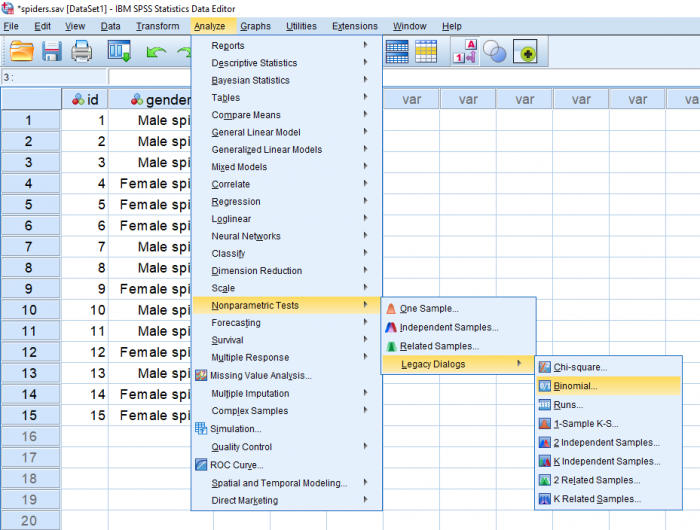
به منظور دسترسی به آزمون دوجمله‌ای در SPSS بهتر است مطابق تصویر بالا عمل کنید و از فهرست Analysis، گزینه Nonparametric Tests و انتخاب Legacy Dialogs و دستور Binomial را اجرا کنید. به این ترتیب پنجره مربوط به اجرای آزمون دوجمله‌ای مطابق باتصویر زیر ظاهر خواهد شد.

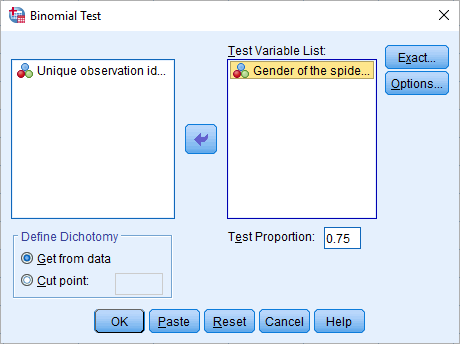همانطور که در تصویر بالا مشاهده می‌کنید، متغیر جنسیت عنکبوت‌ها در کادر Test Variable List قرار گرفته تا نشان دهد که آزمون باید برای این متغیر اجرا شود. در کادر test Proportion نیز مقداری که برای احتمال در فرض صفر در نظر گرفته شده، وارد می‌شود. با توجه به صورت مسئله این مقدار  ثبت شده است. به این ترتیب فرضیات مربوط به این مسئله در زیر دیده می‌شود.

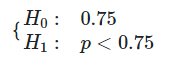اگر لازم است می‌توانید با استفاده از کادر Define Dichotomy مشخص کنید که متغیر معرفی شده دو مقداری است یا باید توسط یک نقطه برش به دو گروه تفکیک شود. برای این کار کافی است با انتخاب Cut point مقداری که محل برش را تعیین می‌کند، مشخص کنید.

نکته: اگر از پنجره Syntax و کد نویسی در SPSS استفاده می‌کنید، کافی است دستورات زیر را به کار برید.

با فشردن دکمه OK خروجی این آزمون به صورت زیر خواهد بود. مشخص است که با توجه به مقدار Sig و مقایسه آن با $$\alpha =\mathrm{۰٫۰۵}$$ فرض صفر را رد نخواهیم کرد زیرا به نظر می‌رسد که مقدار احتمال (Exact Sig) از احتمال خطای نوع اول () بیشتر است. پس نمونه دلیلی برای رد فرض صفر ارائه نکرده است.

نکته: باید توجه داشت که آزمون دو جمله‌ای، اولین مقدار در ستون متغیر را به عنوان موفقیت در نظر می‌گیرد. بنابراین از آنجایی که برای اولین مشاهده مقدار جنسیت برابر با ۱ یعنی عنکبوت نر ثبت شده، آزمون در مورد نسبت عنکبوت‌های نر خواهد بود.

در جدول Binomial Test مشخص است که در ستون Observed Prop برای مشاهده عنکبوت ماده حدود  و برای عنکبوت نر برابر با  است. فاصله مقدار  تا  باعث نشده است تا فرض صفر رد شود. در نتیجه اختلاف بین درصدها بین فرض صفر و نتیجه حاصل از نمونه، ناشی از خطای نمونه‌گیری است و این اختلاف در جامعه آماری وجود ندارد. به این معنی که درصد عنکبوت‌های نر در جامعه آماری همان نسبت  است. باز هم توجه داشته باشید که در پانوشته جدول Binomial Test مشخص شده که فرض مقابل به صورت $$<0.75$$ است در نتیجه آزمون یک طرفه خواهد بود.

حال در نظر بگیرید که قرار است آزمون را برای نسبت عنکبوت‌های ماده اجرا کنیم. کافی است هفت مشاهده اول را برای عنکبوت‌های ماده و هشت مشاهده بعدی را برای عنکبوت‌های نر در نظر بگیریم. به این ترتیب می‌توانیم با استفاده از وزن‌‌دهی به مشاهدات این اطلاعات را به طور خلاصه در SPSS‌ وارد کنیم. به تصویر زیر دقت کنید.

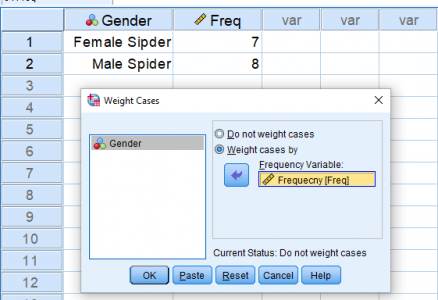با این کار فراوانی‌ها را در ستون Freq و مقدار را در ستون Gender‌ وارد کرده‌ایم. به این ترتیب مقدار ۰ که برای عنکبوت‌های ماده تعریف شده، هفت بار و مقدار ۱ که برای عنکبوت‌های نر در نظر گرفته شده، ۸ بار در آزمون دو جمله‌ای محسوب می‌شوند.

حال به اجرای آزمون دو جمله‌ای بر این اساس می‌پردازیم. مشخص است که با توجه به اینکه اولین مقدار مربوط به عنکبوت‌های ماده است، نسبت این گونه از عنکبوت‌ها در آزمون دو جمله‌ای مورد بررسی قرار می‌گیرد. نتیجه اجرا در این صورت مطابق با تصویر زیر است.

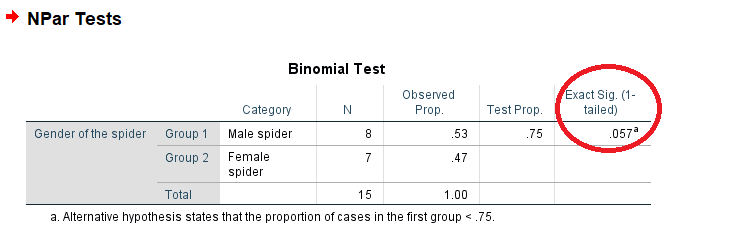با توجه به آزمون یکطرفه و مقدار Exact Sig که در ستون آخر جدول Binomial Test نوشته شده، در سطح خطای  فرض صفر رد می‌شود.

در نتیجه نمی‌توان درصد عنکبوت‌های ماده را برابر با  در نظر گرفت.

آنچه که گفته شد، مسیر دسترسی به دستور مستقیم آزمون دو جمله‌ای و شکل و شیوه تفسیر خروجی‌های آن بود.

شیوه جدید دسترسی مستقیم آزمون دو جمله ای:

می‌توانید گزینه One Sample را از گزینه Nonparametric Tests انتخاب کرده و تنظیمات را به شکلی در‌آورید که آزمون دو جمله‌ای اجرا شود. ابتدا لازم است که نوع آزمون را مشخص کنید. در تصویر زیر درخواست شده که آزمون توسط کاربر انتخاب شود زیرا گزینه Customize Analysis‌ فعال شده است.

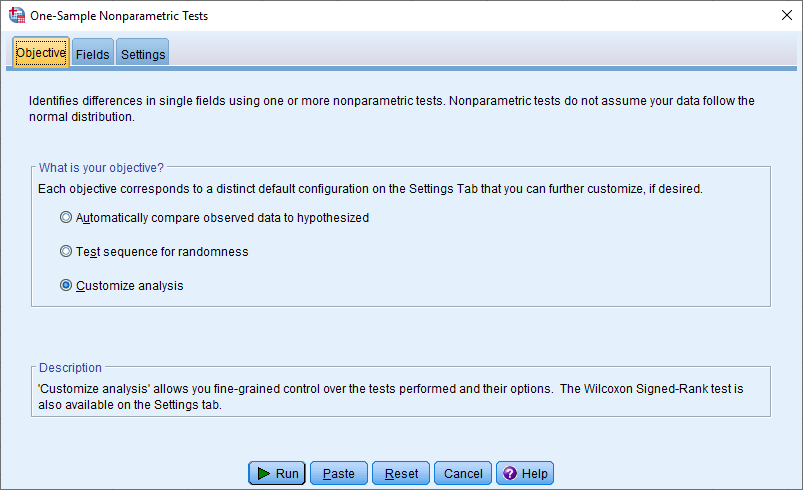
با انتخاب برگه Fields، متغیرهایی که باید در آزمون به کار گرفته شوند، تعیین می‌شود. البته ممکن است SPSS با توجه به نقشی که هر یک از متغیرها دارند، بطور خودکار این کار را انجام دهد. واضح است که متغیر Gender باید به عنوان متغیر مورد نظر انتخاب شود.

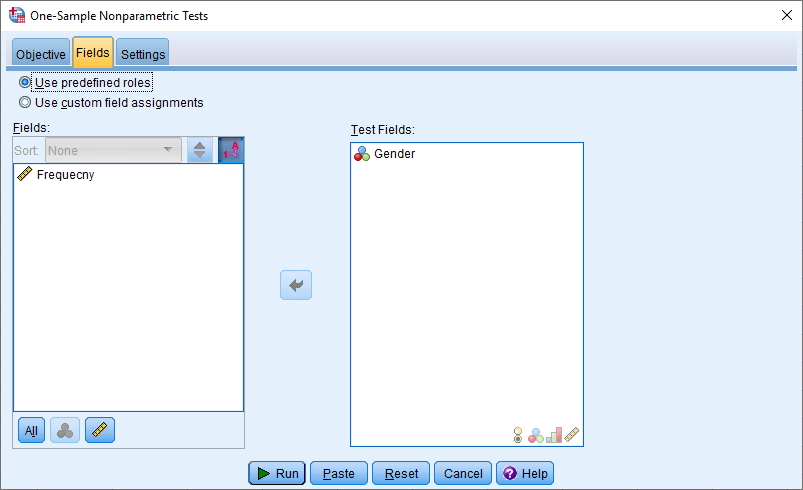
در بخش انتهایی نیز باید نوع آزمون و شیوه اجرای آن تنظیم شود. برگه Settings این وظیفه را به عهده دارد. بنابراین با انتخاب گزینه Customize tests و (Compare observed binary probability to hypothesized (binomial test نوع آزمون را دو جمله‌ای مشخص خواهید کرد.

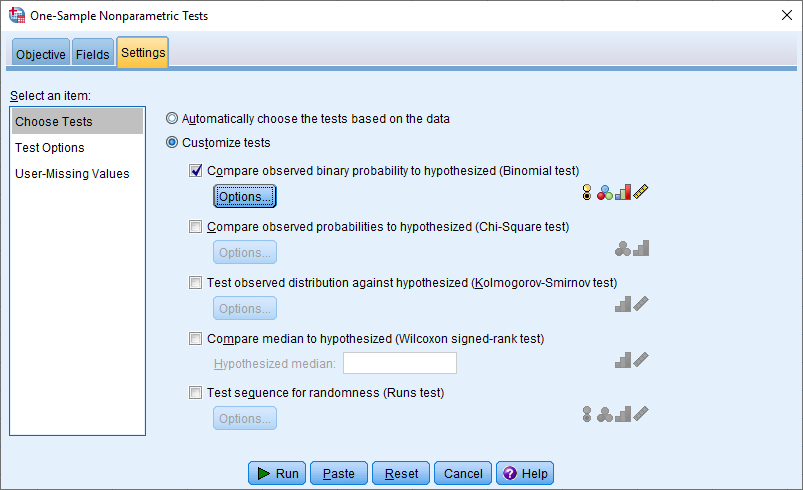
اگر لازم است تنظیماتی نظیر تعیین مقدار احتمال در فرض صفر یا انتخاب مقدار متغیر به عنوان مقدار موفقیت صورت بگیرید از دکمه Options مربوط به این آزمون استفاده کنید. برای پاسخ به مسئله مربوط به عنکبوت‌های ماده کافی است تنظیمات را مطابق با تصویر زیر تعیین کنید.

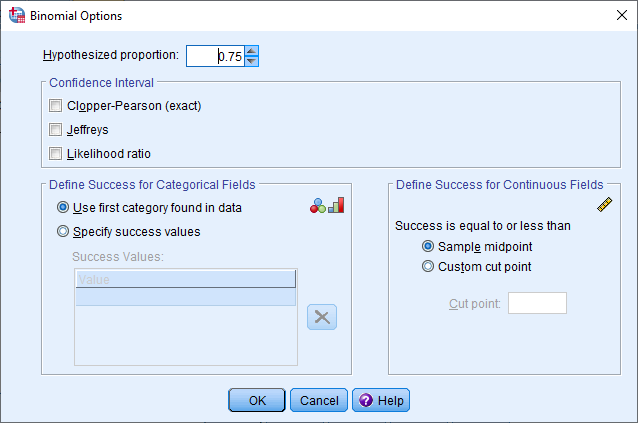با فشردن دکمه Run در پنجره اصلی، آزمون اجرا شده و نتایج مطابق با تصویر زیر ظاهر خواهند شد. البته توجه دارید که باید نتیجه‌ها مطابق با مثال قبل باشند.

خروجی‌هایی که توسط دستورات جدید در SPSS ایجاد می‌شوند، شامل اطلاعاتی بیشتری نیز هستند. همانطور که می‌بینید در ستون Decision مشخص است که فرض صفر در سطح خطای  رد می‌شود.

البته با توجه به ستون Sig این امر مطابق با خروجی‌های قبلی همین نتیجه را خواهد داد. اگر روی این جدول دوبار کلیک کنید، وارد صفحه‌ای می‌شوید که اطلاعات بیشتری در مورد آزمون و متغیرها در خود دارد. چنین پنجره‌هایی به Model Viewer معروف هستند. در تصویر زیر پنجره‌ Model Viewer برای آزمون دو جمله‌ای را می‌بینید

. سمت راست نمودارها و آماره‌های توصیفی و سمت چپ نیز نتیجه اجرای آزمون دو جمله‌ای دیده می‌شود.

09357258425 

www.pajuha.ir

[e-mail]

سفارش ترجمه تخصصی

آزمون میانگین نمونه‌ تکی در SPSS

تعریف آزمون میانگین نمونه‌ تکی در SPSS:

 با یک نمونه از جامعه آماری سروکار خواهیم داشت. قرار است براساس این نمونه در مورد میانگین جامعه قضاوت انجام گیرد.

فرض کنید به عنوان یک تحلیل‌گر داده (Data Scientist)، با یک جامعه‌ آماری مواجه شده‌اید که میانگین آن مشخص نیست و می‌خواهید در مورد این میانگین، تحقیق و بررسی انجام دهید و به یک تصمیم برسید.

 مثال:

در نظر بگیرید که در یک کارخانه تولیدی لبنیات، شکایاتی مبنی بر کم بودن وزن بسته‌های پنیر دریافت شده است. مسئولین برای آنکه مشخص کنند آیا شکایات معتبر یا بی‌دلیل هستند دست به نمونه‌گیری زده‌اند و براساس اطلاعاتی که از وزن بسته‌های پنیر در نمونه وجود دارد، می‌خواهند به این تصمیم آماری برسند که آیا دستگاه‌ها احتیاج به تنظیم دارند یا شکایات بی‌مورد هستند.

پیش فرض‌های تحلیل t تک نمونه ای یا تی تک گروهی

۱- توزیع داده‌ها باید نرمال باشد (با استفاده از آزمون کولموگروف اسمیرنوف).

۲- داده‌ها باید در مقیاس فاصله‌ای یا نسبی باشند (ماننده نمره سن، وزن، پرسشنامه و …).

۳- نمره معیار یا ثابتی باشد که بتوانید میانگین خود را با آن مقایسه کنید.

اجرای تحلیل t تک نمونه ای یا تی تک گروهی

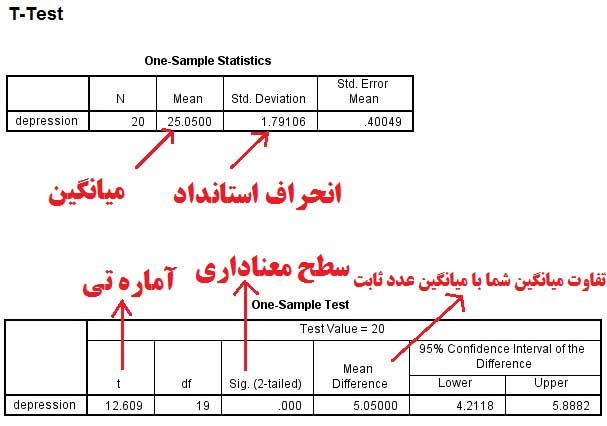
فرض کنید نمره افسردگی چند نفر را با پرسشنامه افسردگی بک به دست آورده‌اید. طبق دستورالعمل این پرسشنامه افرادی که نمره ۲۰ و بالاتر را کسب کنند دارای افسردگی هستند. حالا شما می‌خواهید نمره‌ای که به دست آوردید را با این عدد ثابت ۲۰ مقایسه کنید. برای این کار در منوی بالای SPSS به مسیر زیر بروید:

Analyze>Compare Means>One-Sample T Test

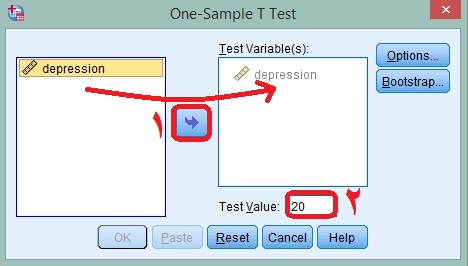
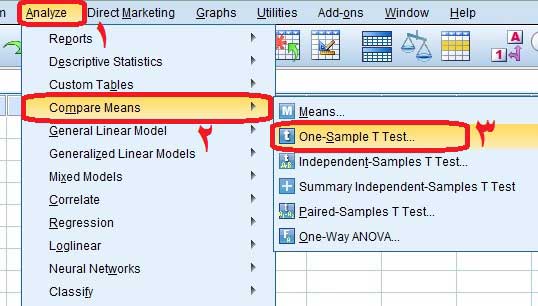پس از رفتن به مسیر ذکر شده کادر زیر برای شما باز خواهد شد. در کادر زیر نمره افسردگی را از کادر سمت چپ به کادر سمت راست انتقال می‌دهیم.  سپس در کادر Test Value که در شکل زیر با عدد ۲ مشخص شده است نمره ثابت یا معیار را که در اینجا ۲۰ است وارد می‌کنیم و بر روی گزینه Ok کلیک می‌کنیم.

پس از مرحله بالا خروجی داده‌ها ظاهر می‌شود. در بین جداول، نمرات و اعداد مشخص شده به رنگ قرمز موررد نظر ما هستند و در جدول خروجی گزارش می‌شوند. همانگونه که در جدول زیر مشاهده می‌شود میانگین به دست آمده از جانب ما از نمره ثابت به طور معناداری بیشتر است.

(نحوه گزارش خروجی تحلیل t تک نمونه ای یا تی تک گروهی در SPSS)

1. پیش‌نیازهای ضروری برای آزمون میانگین نمونه تکی (One Sample T Test)

قبل از هر چیز باید از شرایط و فرضیاتی که آزمون میانگین نمونه تکی باید داشته باشد مطلع باشیم. در زیر فهرستی از این فرضیات دیده می‌شود:

• داده‌ها کمی (عددی) هستند.
• توزیع جامعه آماری نرمال است.
• واریانس جامعه آماری ثابت ولی نامعلوم است. این پارامتر باید توسط مشاهدات نمونه‌ای محاسبه یا برآورد شود.

نکته:

اگر حجم نمونه کم (حدود ۳۰) و میزان چولگی، کم باشد، باز هم می‌توان از آزمون میانگین نمونه‌ تکی برای قضاوت در مورد میانگین جامعه استفاده کرد.

فرض‌ها و آماره آزمون

در انجام آزمون میانگین نمونه‌ تکی، فرض‌های صفر و مقابل به صورت زیر در نظر گرفته می‌شوند:

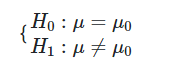
مقدار $${\mu }_{\mathrm{۰}}$$ همان مقداری است که به نظر می‌رسد باید میانگین جامعه آماری داشته باشد. حتی می‌توان آن را به عنوان حدس اولیه برای میانگین جامعه در نظر گرفت. مشخص است که در فرض مقابل یا $$H_1$$ این تصور به چالش کشیده شده است. آماره آزمون، در ادامه معرفی شده و دارای توزیع t student است.

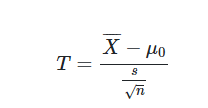
نکته: در نرم‌افزار SPSS فرضیات، به صورت زیر در نظر گرفته می‌شوند. ولی به هر حال نتیجه حاصل، در هر دو حالت یکسان خواهد بود.

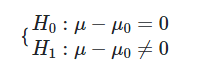
با توجه به خصوصیاتی که مقدار احتمال (p-value) دارد، اگر نتیجه آن برای آزمون کمتر از احتمال خطای نوع اول () یا همان سطح خطای آزمون شود، فرض صفر را رد خواهیم کرد.

شیوه اجرای آزمون میانگین نمونه تکی در SPSS

برای اجرای این آزمون طبق معمول از فهرست Analysis شروع می‌کنیم سپس گزینه Compare Means و دستور One Sample T-test را انتخاب کرده و پارامترهای آزمون را مطابق تصویرهای زیر تنظیم خواهیم کرد.

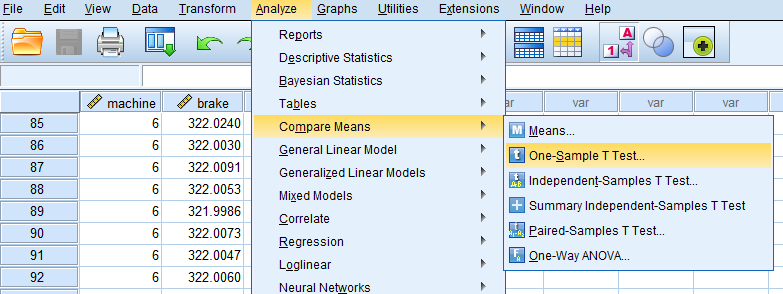
در تصویر زیر هر یک از پارامترهای مربوط به این آزمون، معرفی شده‌اند. توجه داشته باشید که متغیرهایی که در قسمت (Test Variable(s قرار می‌دهید، مقدارهای عددی یا متغیر کمی باشند.

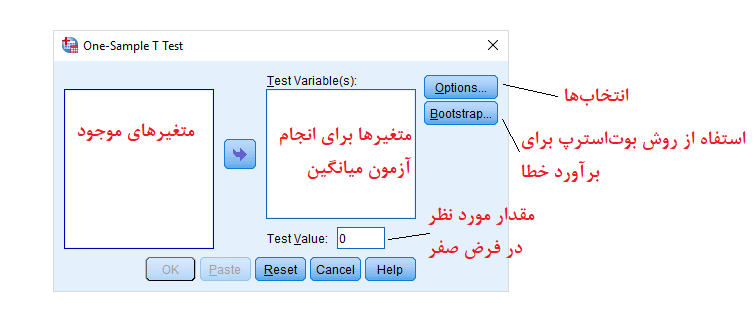
در خروجی این آزمون، یک فاصله اطمینان برای اختلاف میانگین جامعه از $${\mu }_{\mathrm{۰}}$$ نیز ایجاد می‌شود. سطح اطمینان برای این فاصله اطمینان را با انتخاب دکمه Options می‌توان تعیین کرد.

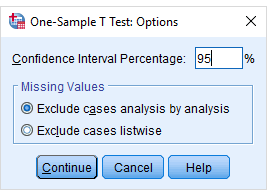
همینطور اگر چندین متغیر را در بخش متغیرهای آزمون قرار داده‌اید، با انتخاب گزینه‌ Exclude cases analysis by analysis مشخص می‌کنید که داده‌های گمشده (Missing Values) در هر تحلیل جداگانه در نظر گرفته شود.

برای مثال اگر برای متغیر اول،‌ مشاهده سوم و برای متغیر دوم، مشاهده پنجم دارای مقدار گمشده است، هنگام اجرای آزمون برای متغیر اول، مشاهده سوم و برای آزمون میانگین متغیر دوم،‌ مشاهده پنجم در نظر گرفته نخواهد شد. ولی با انتخاب Exclude cases listwise فقط مشاهداتی در انجام همه آزمون‌ها به کار می‌روند که مقدار گمشده در هیچ یک از آن‌ها وجود ندارد. بنابراین با انتخاب این گزینه، مشاهده سوم و پنجم در تحلیل به کار نخواهند رفت.

مثال ۲

فرض کنید اطلاعات مربوط به وزن ۲۰ بسته ۷۵۰ گرمی پنیر تولیدی در یک کارخانه در اختیار شما قرار گرفته است. باید قضاوت کنید که آیا این نمونه در مورد شکایت مشتریان مبنی بر کم بودن وزن بسته‌ها دلیل خوبی است یا شکایت‌ها بی‌مورد هستند؟ این اطلاعات را در SPSS مطابق تصویر زیر وارد کرده‌ایم.

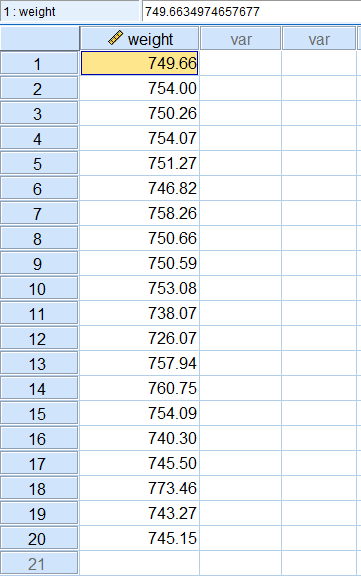
برای آنکه مشخص شود توزیع این داده‌ها شبیه نرمال هستند، از یک «بافت‌نگار فراوانی» (Histogram) استفاده می‌کنیم. برای ترسیم آن از فهرست Analysis گزینه frequency را انتخاب و در پنجره ظاهر شده تنظیمات را مطابق با تصویرهای زیر پیاده می‌کنیم.

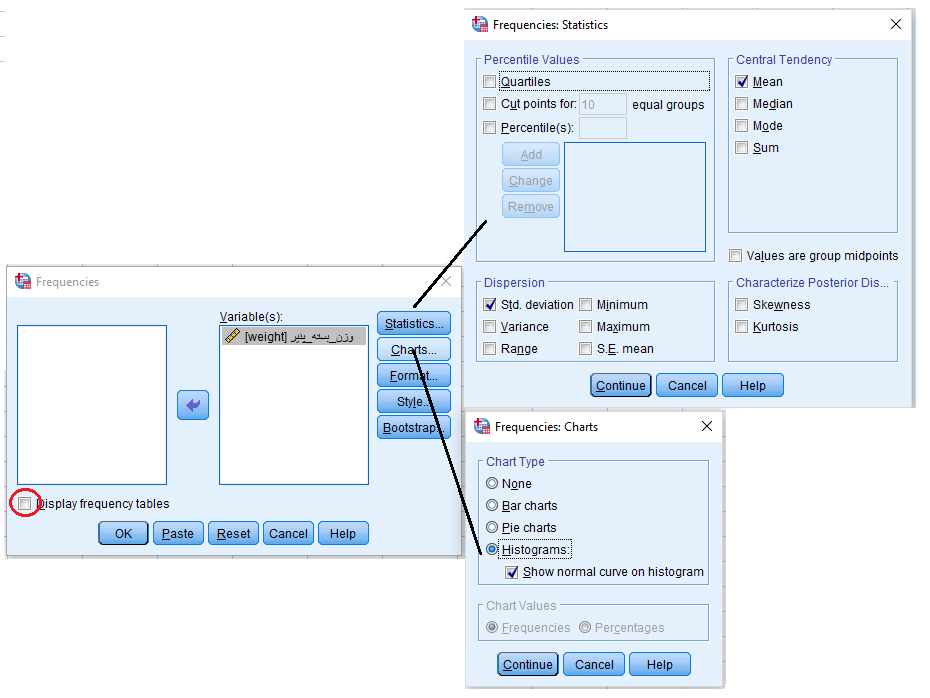
نکته:

از آنجایی که احتیاجی به مشاهده جدول فراوانی وجود ندارد، گزینه display frequency tables را از حالت انتخاب خارج کرده‌ایم.

(خروجی به صورت زیر در خواهد آمد.)

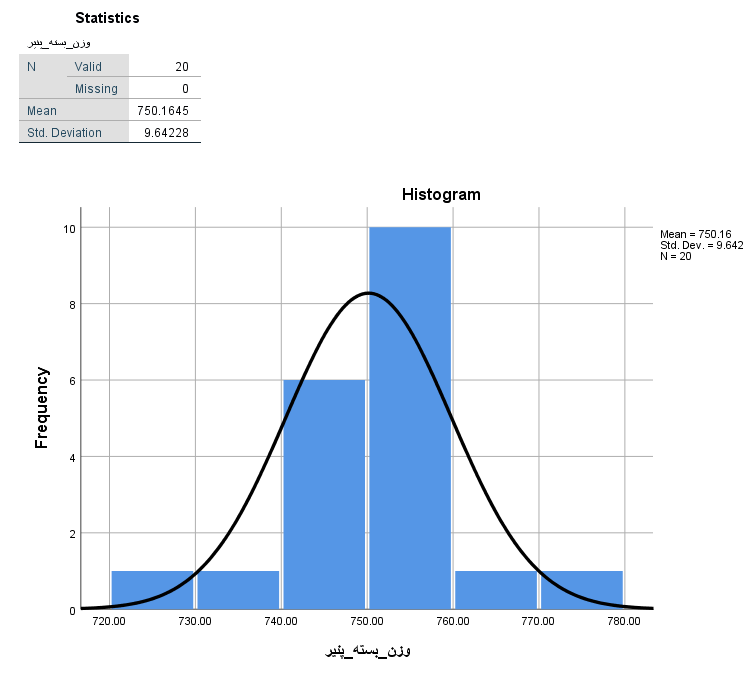
• حال مراحل دسترسی به آزمون میانگین نمونه تکی را طی کرده و پارامترها را مطابق تصویر زیر در پنجره مربوط به آزمون تنظیم می‌کنیم.

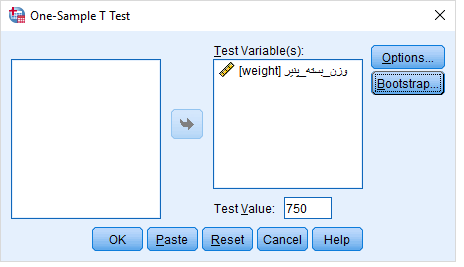
• با فشردن دکمه OK محاسبات صورت گرفته و خروجی مطابق با جدول زیر ظاهر خواهد شد.

1. در جدول اول با عنوان One-Sample Statistics،

2. میانگین نمونه برابر با ۷۵۰٫۱۶۴۵ گرم

3. با انحراف استاندارد  ۹٫۶۴۲۲۸ گرم

4. خطای استاندارد میانگین نیز برابر با ۲٫۱۵۶۰۸ گرم

• در جدول دوم، آزمون آماری با فرض صفر:

1.  مقدار آمار آزمون ۰٫۰۷۶ و درجه آزادی نیز ۱۹ بدست می آید.

2. با توجه به بزرگ بودن مقدار احتمال (p-Value) که در SPSS با Sig نمایش داده می‌شود و مقایسه آن با احتمال خطای نوع اول دلخواه $$\alpha$$ (که معمولا آن را ۰٫۰۵ در نظر می‌گیریم)

3. متوجه می‌شویم که ادعا مشتریان نادرست است چرا؟

4. زیرا ۰٫۹۴۰ بزرگتر از ۰٫۰۵ است. در نتیجه این نمونه دلیلی بر رد فرض صفر ارائه نکرده است و نمی‌توان فرض صفر را رد کرد.

مثال ۳:

.فرض کنید دو نوع محصول A و B در بسته‌های ۷۵۰ گرمی تولید شوند.

از هر دو محصولات آزمون می گیریم که متوسط وزن بسته‌ها همان ۷۵۰ گرم است.

ولی بنا به دلایلی (مثلا باز بودن بسته بندی و خارج شدن محتویات از بسته‌ها) در هر دو نمونه یک مقدار گمشده وجود دارد.

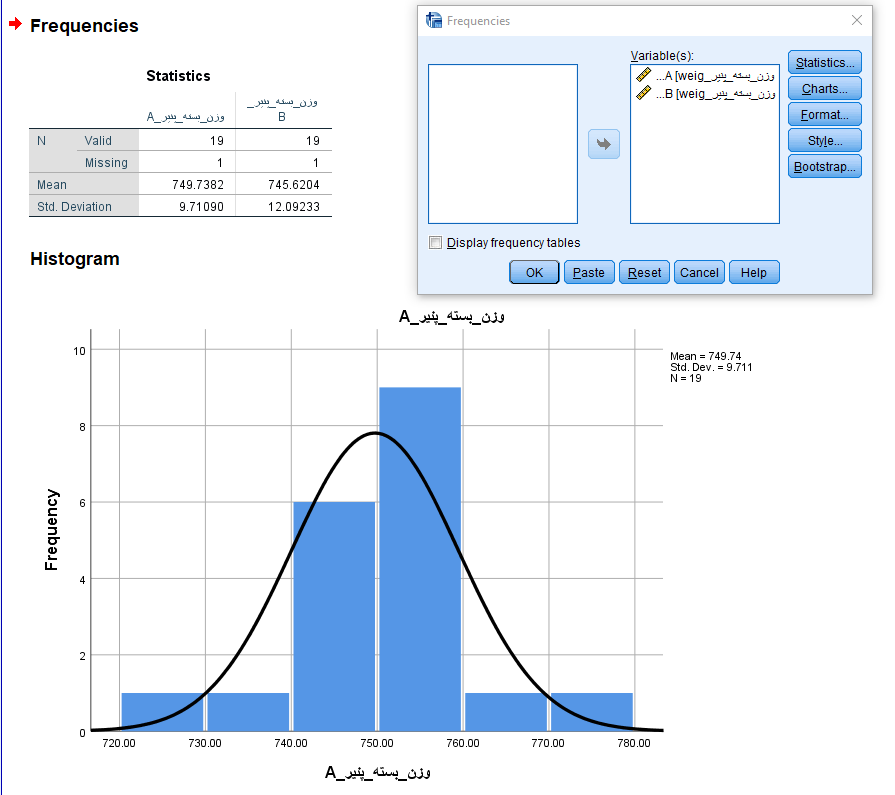
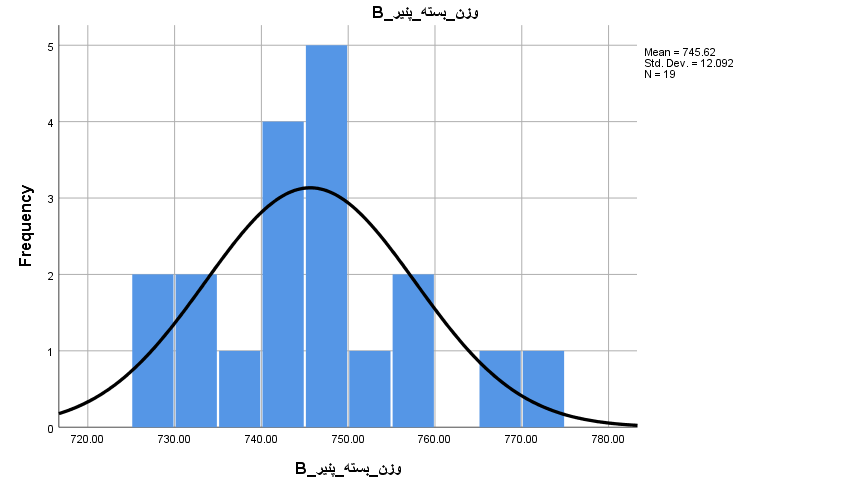
حال آزمون را با دو وضعیت برای داده‌های گمشده اجرا می‌کنیم. در حالت اول گزینه Exclude cases analysis by analysis را در بخش option فعال کرده و نتایج آزمون را مشاهده می‌کنیم.

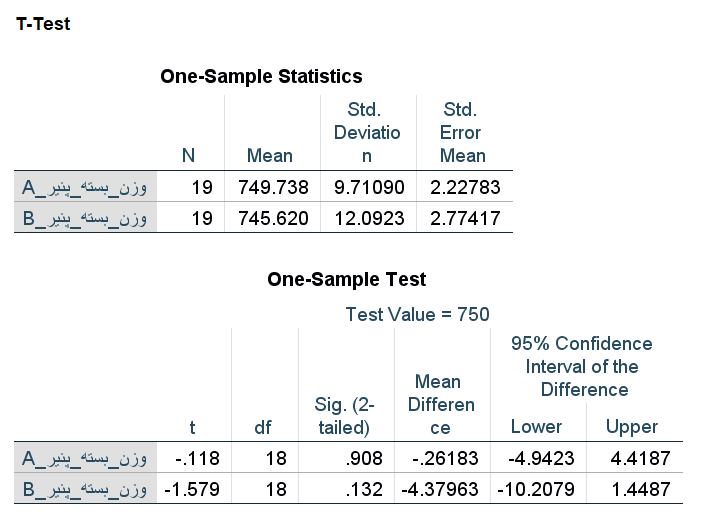
از آنجایی که هر کدام از متغیرها یا ستون‌ها دارای یک مشاهده گمشده بودند، تعداد در جدول اول برابر با ۱۹ ثبت شده است.

همچنین در جدول دومی SIG،  فرض صفر در سطح خطای ۰٫۰۵، توسط این نمونه‌ها رد نخواهد شد و به نظر می‌رسد میانگین وزن بسته‌ها همان ۷۵۰ گرم ادعای کارخانه است.

نکته :اگر لازم باشد که هر دوی مشاهدات گمشده در متغیرها کارخانه لحاظ نشوند چه کار باید انجام داد؟

کافی است که گزینه Exclude cases listwise را از بخش options انتخاب و آزمون را اجرا کنید.

خروجی در این حالت به صورت زیر در خواهد آمد. مشخص است که در جدول اول، تعداد مربوط به هر دو گروه ۱۸ خواهد بود و درجه آزادی (df) مربوط به آماره آزمون هم ۱۷ محاسبه می‌شود.

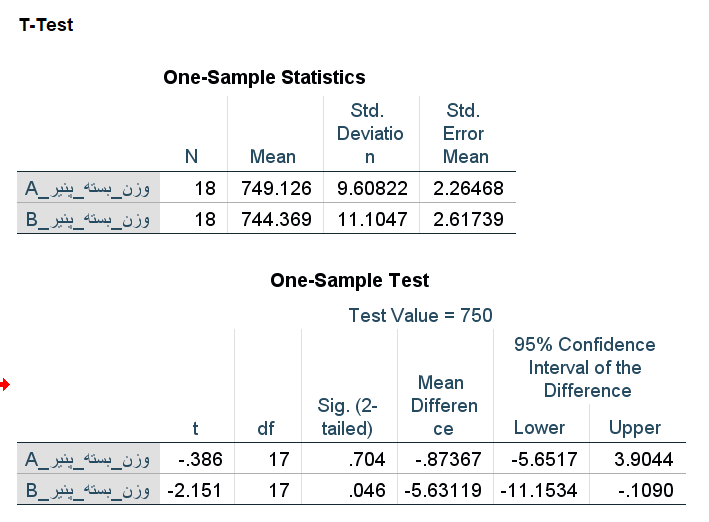
نکتهمهم:تغییر مقدار میانگین در هر دو متغییر فوق:

۱-  تعداد مشاهدات متفاوت است، میانگین نیز  بر اساس آن تغییر کرده است.

۲-چرا در کار خانه وزن بسته‌های محصول B کمتر از ۷۵۰ گرم است؟

زیرا مقدار Sig در سطر دوم با احتساب داده‌های گمشده برای هر دو گروه کمتر از ۰٫۰۵ است. بنابراین فرض صفر رد می شود یعنی میانگین بسته‌های محصول B مخالف ۷۵۰ گرم است.

از طرف دیگر چون فاصله اطمینان شامل ناحیه منفی است مشخص می شود که تفاضل میانگین وزن بسته‌ها از ۷۵۰ گرم دد ۹۵٪ مواقع کمتر از صفر است. به این ترتیب مشخص است که وزن بسته‌ها کمتر از ۷۵۰ گرم است و دستگاه‌های مربوط به بسته‌بندی باید تعمیر و تنظیم شوند.

09357258425 

www.pajuha.ir

[e-mail]

سفارش ترجمه تخصصی

نحوه رسم نمودار میله ای در spss

• تعریف نمودار میله ای در spss :

نمودار ستونی شامل مجموعه ای از ستون ­هاست که با فاصله یکنواختی در کنار هم قرار می­ گیرند و هر ستون مختصّ یک طبقه از متغیر و طول آن متناسب با فراوانی یا درصد آن طبقه است.
نمودار ستونی برای متغیرهای کیفی (اسمی و ترتیبی) به­ کار می­ رود، اما برای متغیر کمّی که تعداد طبقات آن کم باشد هم قابل استفاده است.

به عنوان مثال چنانچه متغیری به نام تعداد فرزند داشته باشیم و در نمونه نهایی تعداد فرزندان هر خانواده از ۱ تا ۵ فرزند باشد و در واقع تعداد فرزندان شامل ۵ طبقه باشد بازهم می ­توانیم از این نمودار استفاده کنیم. در مثال کتاب، می ­توان برای متغیرهای تحصیلات پدر، قومیت و درآمد اقدام به ترسیم نمودار ستونی نمود.

نحوه رسم نمودار میله ای در spss

در این نوع نمودار، هر میله متناظر با یک رده از توزیع کیفی است.

(تفاوت )در آرایش میله ها باید جنبه های مختلفی را مورد توجه قرار داد:

1. میله ها فقط در طول با هم تفاوت دارند و نه در پهنا.
2. فضایی بین دو میله متوالی منظور شده است تا تعیین میله را با نشان آن ساده تر کند.
3. برای تسهیل تحلیل، میله ها به ترتیب بزرگی رده بندی می شوند، که ممکن است کاهشی یا افزایشی باشد.
4. وقتی مقایسۀ تصویری دو یا چند توزیع کیفی مورد نظر باشد، اغلب می توان نمودارهای میله ای آن ها را ترکیب کرد.

مثال:

توزیع کیفی شرکت ها با توجه به نوع صنعت به صورت جدول ۲-۳ رده بندی شده اند.

مراحل رسم نمودار میله ای (ستونی) در spss

۱- داده ها را به spss معرفی کنید.

۲- دستور Tranform > compute variable…را اجرا کنید.

۳- در ناحیۀ target variable (متغیر هدف)، از پنجرۀ ، متغیری به نام PCCount (درصد تعداد شرکت) تعریف کنید.

۴- در ناحیۀ Numeric Expression (عبارت عددی) جمله را به صورت (CCount)/ 383 تکمیل کنید، شکل ۵-۳٫

۱- در پنجرۀ compute variable روی ok کلیک کنید. متغیر PCCount در پنجرۀ spss ایجاد می شود.

۲- دستور Graphs > Legacy Dialogs > Bar …را اجراکنید.

۳- مطمئن باشید در پنجرۀ Bar Charts (نمودارهای میله ای) عبارت Simple انتخاب شده است (در این حالت دور نماد مربوطه، یک کادر مربعی سیاه رنگ نشان داده می شود.

۴- با کلیک دکمۀ Define (تعریف)، پنجرۀ define simple bar: summaries of Groups of cases را باز کرده و عبارت PCCount را به ناحیۀ category Axis (محور طبقه بندی) منتقل کنید، شکل ۶-۳٫

۵- روی دکمۀ ok کلیک کنید، خروجی ۲-۳٫

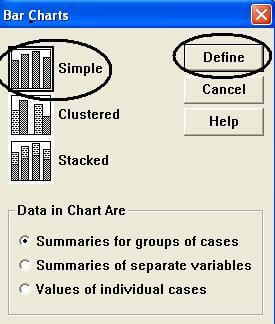
توجه شود:

برای رسم نمودار «میله ای خوشه ای» (clustered Bar)، در پنجرۀ bar charts، نوع clustered را انتخاب کنید.

برای رسم نمودار «میله ای انباشته ای» (stacked bar) در پنجرۀ bar charts نوع stacked را انتخاب کنید.

 فرض کنید یک نظر سنجی در مورد سبک فیلم مورد علاقه‌ افراد، انجام داده‌اید تا بدانید که کدام سبک فیلم طرفدار بیشتری دارد:

جدول سبک فیلم‌های مورد علاقه
کمدی	اکشن	رمانتیک	درام	علمی-تخیلی
۴	۵	۶	۱	۴

این جدول را می‌توانیم روی یک نمودار میله‌ای به شکل زیر نمایش دهیم:

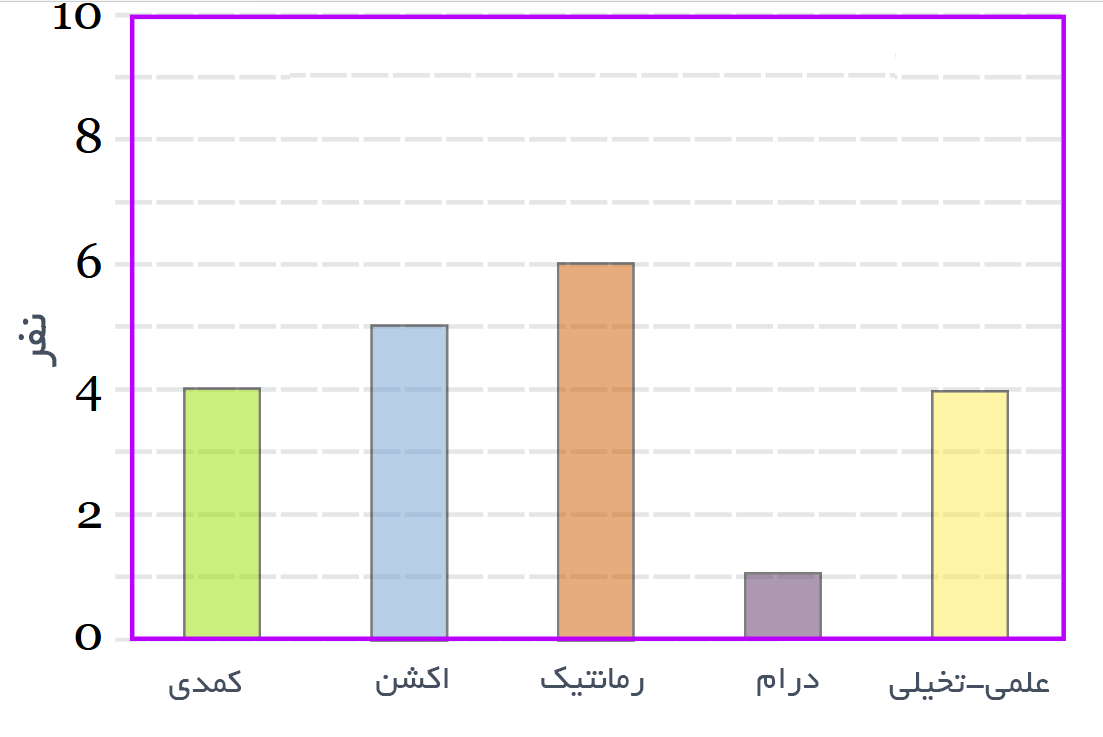
این روشی بسیار خوب برای نمایش اندازه‌های نسبی است، چون می‌توانیم با نگاهی مختصر دریابیم که کدام سبک فیلم‌ها طرفدار بیشتر و کدام ها طرفدار کمتری دارند. همچنین از نمودارهای میله‌ای می‌توانیم برای نمایش اندازه نسبی بسیاری از چیزها، مانند مدل ماشینی که مردم استفاده می‌کنند، یا تعداد مشتریان یک مغازه در روزهای مختلف و یا موارد بی‌شمار‌ دیگر  استفاده کنیم.

مثال: بهترین میوه

نتیجه یک نظرسنجی از ۱۴۵ نفر با سوال «کدام میوه از نظر شما بهترین است؟» به صورت زیر بوده است:

میوه:	سیب	پرتقال	موز	کیوی	بلوبری	انگور
نفر:	۳۵	۳۰	۱۰	۲۵	۴۰	۵

نمودار میله‌ای داده‌های فوق به صورت زیر است:

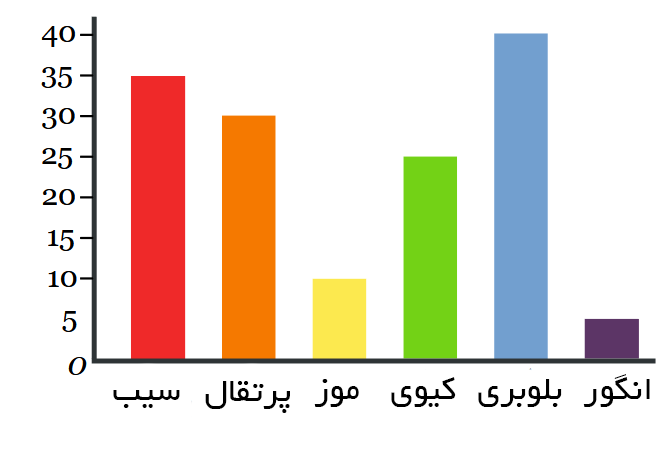
این گروه از مردم فکر می کنند که بلوبری بهترین میوه است. نمودار های میله‌ای می‌توانند مانند تصویر زیر به صورت افقی نیز باشند:

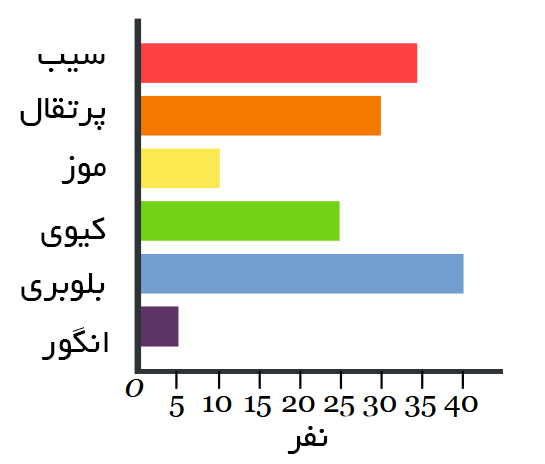
مثال: نمرات دانش‌آموزان

در یک امتحان، این تعداد از دانش آموزان، نمرات زیر را کسب کرده‌اند:

نمره:	A	B	C	D
تعداد دانش‌آموز:	۴	۱۲	۱۰	۲

و نمودار میله‌ای نیز چنین است:

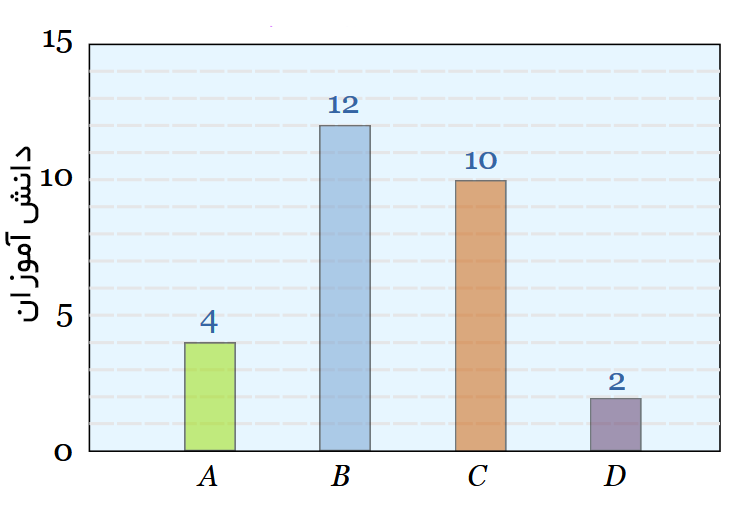
هیستوگرام‌ها در مقابل نمودارهای میله‌ای

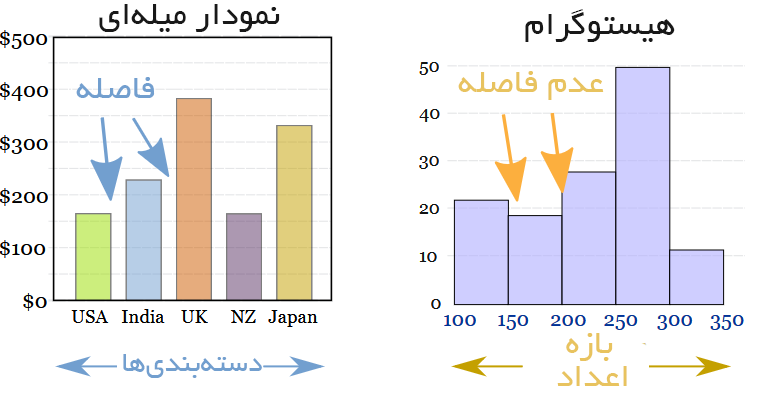
نمودار های میله‌ای در مواردی مناسب هستند که داده‌ها دسته‌بندی شده باشند، مانند کمدی، درام و غیره. اما اگر داده‌های پیوسته‌ای مانند قد یک شخص دارید بهتر است از هیستوگرام استفاده کنید. همچنین به طور معمول بین ستون‌ها در نمودار‌های میله‌ای فواصل مناسبی قرار می‌گیرند تا شبیه هیستوگرام نباشند و باعث اشتباه نشوند.

نکته مهم:

نمودار میله ای خطا در spss

یک جایگزین مناسب برای نمودار میله ای، نموداری به نام Error bar (میله ای خطا) است که در آن میانگین مقادیر هر طبقه با یک نقطه و «واریانس» آن توسط یک خط عمودی نشان داده می شود که از داخل نقطه می گذرد.

09357258425 

www.pajuha.ir

[e-mail]

سفارش ترجمه تخصصی